
12.有两排座位,前排11个座位,后排12个座位,现安排2人就座,规定前排中间的3个座位不能坐,并且这2人不左右相邻,共有多少种不同排法?
解 ∵前排中间3个座位不能坐,
∴实际可坐的位置前排8个,后排12个.
(1)两人一个前排,一个后排,方法数为C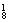 ·C
·C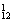 ·A
·A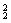 种;
种;
(2)两人均在后排左右不相邻,共A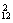 -A
-A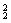 ·A
·A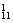 =A
=A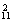 种;
种;
(3)两人均在前排,又分两类:
①两人一左一右,共C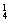 ·C
·C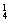 ·A
·A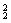 种;
种;
②两人同左同右,有2(A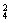 -A
-A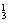 ·A
·A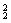 )种.
)种.
综上可知,不同排法种数为
C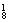 ·C
·C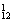 ·A
·A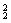 +A
+A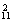 +C
+C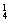 ·C
·C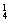 ·A
·A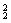 +2(A
+2(A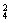 -A
-A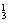 ·A
·A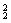 )=346种.
)=346种.
11.已知平面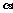 ∥
∥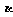 ,在
,在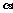 内有4个点,在
内有4个点,在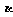 内有6个点.
内有6个点.
(1)过这10个点中的3点作一平面,最多可作多少个不同平面?
(2)以这些点为顶点,最多可作多少个三棱锥?
(3)上述三棱锥中最多可以有多少个不同的体积?
解 (1)所作出的平面有三类:①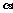 内1点,
内1点,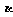 内2点确定的平面,有C
内2点确定的平面,有C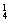 ·C
·C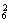 个;②
个;②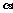 内2点,
内2点,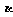 内1点确定的平面,有C
内1点确定的平面,有C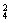 ·C
·C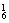 个;③
个;③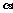 ,
,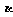 本身.
本身.
∴所作的平面最多有C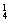 ·C
·C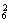 +C
+C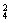 ·C
·C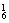 +2=98(个).
+2=98(个).
(2)所作的三棱锥有三类:①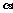 内1点,
内1点,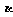 内3点确定的三棱锥,有C
内3点确定的三棱锥,有C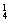 ·C
·C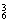 个;②
个;②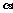 内2点,
内2点,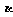 内2点确定的三棱锥,有C
内2点确定的三棱锥,有C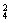 ·C
·C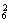 个;
个;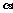 内3点,
内3点,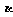 内1点确定的三棱锥,有C
内1点确定的三棱锥,有C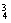 ·C
·C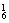 个.
个.
∴最多可作出的三棱锥有:C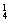 ·C
·C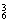 +C
+C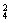 ·C
·C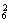 +C
+C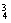 ·C
·C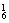 =194(个).
=194(个).
(3)∵当等底面积、等高的情况下三棱锥的体积相等,
且平面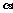 ∥
∥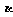 ,∴体积不相同的三棱锥最多有
,∴体积不相同的三棱锥最多有
C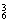 +C
+C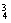 +C
+C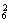 ·C
·C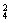 =114(个).
=114(个).
10.课外活动小组共13人,其中男生8人,女生5人,并且男、女各指定一名队长,现从中选5人主持某种活动,依下列条件各有多少种选法?
(1)只有一名女生;
(2)两队长当选;
(3)至少有一名队长当选;
(4)至多有两名女生当选.
解 (1)一名女生,四名男生,故共有C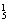 ·C
·C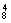 =350(种).
=350(种).
(2)将两队长作为一类,其他11人作为一类,
故共有C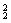 ·C
·C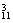 =165(种).
=165(种).
(3)至少有一名队长含有两类:有一名队长和两名队长.
故共有:C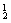 ·C
·C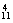 +C
+C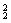 ·C
·C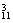 =825(种).
=825(种).
或采用间接法:C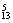 -C
-C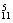 =825(种).
=825(种).
(4)至多有两名女生含有三类:有两名女生、只有一名女生、没有女生.
故选法为C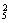 ·C
·C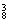 +C
+C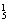 ·C
·C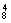 +C
+C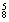 =966(种).
=966(种).
9.某外商计划在4个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,求该外商不同的投资方案有多少种?
解 可先分组再分配,据题意分两类,一类:先将3个项目分成两组,一组有1个项目,另一组有2个项目,然后再分配给4个城市中的2个,共有C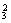 A
A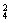 种方案;另一类1个城市1个项目,即把3个元素排在4个不同位置中的3个,共有A
种方案;另一类1个城市1个项目,即把3个元素排在4个不同位置中的3个,共有A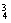 种方案.由分类计数原理可知共有C
种方案.由分类计数原理可知共有C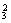 A
A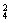 +A
+A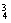 =60种方案.
=60种方案.
8.(2008·浙江理,16)用1,2,3,4,5,6组成六位数(没有重复数字),要求任何相邻两个数字的奇偶性不同,且1和2相邻.这样的六位数的个数是 .(用数字作答)
答案 40
7.平面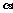 内有四个点,平面
内有四个点,平面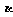 内有五个点,从这九个点中任取三个,最多可确定
个平面,任取四点,最多可确定 个四面体.(用数字作答)
内有五个点,从这九个点中任取三个,最多可确定
个平面,任取四点,最多可确定 个四面体.(用数字作答)
答案 72 120
6.(2008·安徽理)12名同学合影,站成了前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,其他人的相对顺序不变,则不同调整方法的种数是 (用式子表示).
答案 C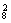 A
A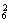
5.(2008·天津理)有8张卡片分别标有数字1,2,3,4,5,6,7,8,从中取出6张卡片排成3行2列,要求3行中仅有中间行的两张卡片上的数字之和为5,则不同的排法共有 种.
答案 1 248
4.在图中,“构建和谐社会,创美好未来”,从上往下读(不能跳读),共有 种不同的读法.

答案 252
3.记者要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有 种.
答案 960
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com