
2.了解小说《红与黑》的故事梗概及时代背景。
1.了解作者斯丹达尔。
3.红与黑
学习目标
1 选择题
选择题
(1)不等式6x2+5x<4的解集为( B )
A (-∞,-
(-∞,-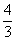 )∪(
)∪(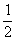 ,+∞) B
,+∞) B (-
(- 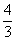 ,
,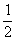 )
)
C (-
(- 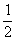 ,
,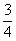 )
D
)
D (-∞,-
(-∞,-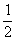 )∪(
)∪(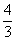 ,+∞)
,+∞)
(2)a>0,b>0,不等式a> >-b的解集为( C )
>-b的解集为( C )
A -
-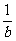 <x<0或0<x<
<x<0或0<x<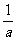 B
B -
- 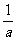 <x<
<x<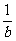
C x<-
x<-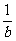 或x>
或x>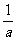 D
D -
- 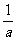 <x<0或0<x<
<x<0或0<x<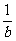
(3)不等式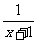 (x-1)(x-2)2(x-3)<0的解集是(
B )
(x-1)(x-2)2(x-3)<0的解集是(
B )
A (-1,1)∪(2,3)
B
(-1,1)∪(2,3)
B (-∞,-1)∪(1,3)
(-∞,-1)∪(1,3)
C (-∞,-1)∪(2,3)
D
(-∞,-1)∪(2,3)
D R
R
(4)若a>0,且不等式ax2+bx+c<0无解,则左边的二次三项式的判别式(C )
A Δ<0 B
Δ<0 B Δ=0 C
Δ=0 C Δ≤0 D
Δ≤0 D Δ>0
Δ>0
(5)A={x|x2+(p+2)x+1=0,x∈R},且R*∩A=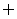 ,则有( B )
,则有( B )
A p>-2 B
p>-2 B p≥0 C
p≥0 C -4<p<0 D
-4<p<0 D p>-4
p>-4
(6)θ在第二象限,cosθ=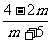 ,sinθ=
,sinθ=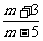 ,则m满足( D )
,则m满足( D )
A m<-5或m>3 B
m<-5或m>3 B 3<m<9 C
3<m<9 C m=0或m=8 D
m=0或m=8 D m=8
m=8
(7)已知不等式loga(x2-x-2)>loga(-x2+2x+3)在x=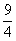 时成立,则不等式的解集为( B)
时成立,则不等式的解集为( B)
A {x|1<x<2}
B
{x|1<x<2}
B {x|2<x<
{x|2<x<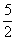 } C
} C {x|1<x<
{x|1<x<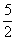 } D
} D {x|2<x<5}
{x|2<x<5}
(8)设0<b<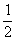 ,下列不等式恒成立的是( C )
,下列不等式恒成立的是( C )
A b3>b
b3>b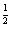 ?B
?B logb(1-b)>1 C
logb(1-b)>1 C cos(1+b)>cos(1-b) D
cos(1+b)>cos(1-b) D (1-b)n<bn,n∈N
(1-b)n<bn,n∈N
(9)若不等式x2-logax<0在(0,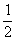 )内恒成立,则a满足( A )
)内恒成立,则a满足( A )
A
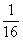 ≤a<1 B
≤a<1 B
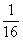 <a<1 C
<a<1 C 0<a≤
0<a≤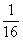 D
D 0<a<
0<a<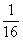
(10)不等式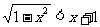 的解集是( A )
的解集是( A )
A [0,1] B
[0,1] B [0,+∞] C
[0,+∞] C (1,+∞) D
(1,+∞) D [-1,1]
[-1,1]
(11)不等式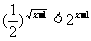 的解集是( D )
的解集是( D )
A
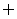 B
B (1,2)
C
(1,2)
C (2,+∞) D
(2,+∞) D (1,+∞)
(1,+∞)
(12)不等式(x-1)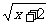 ≥0的解集是( B )
≥0的解集是( B )
A {x|x>1}
B
{x|x>1}
B {x|x≥1或x=-2} C
{x|x≥1或x=-2} C {x|x≥1} D
{x|x≥1} D {x|x≥-2且x≠1}
{x|x≥-2且x≠1}
(13)函数f(x)= 的定义域为A,函数g(x)=
的定义域为A,函数g(x)=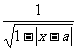 的定义域为B,则使A∩B=
的定义域为B,则使A∩B=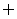 ,实数a的取值范围是( D )
,实数a的取值范围是( D )
A {a|-1<a<3} B
{a|-1<a<3} B {a|-2<a<4} C
{a|-2<a<4} C {a-2≤a≤4} D
{a-2≤a≤4} D {a|-1≤a≤3}
{a|-1≤a≤3}
(14)关于x的不等式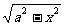 <2x+a(a>0)的解集为( B )
<2x+a(a>0)的解集为( B )
A (0,a) B
(0,a) B (0,a] C
(0,a] C (0,+∞)∪(-∞,-
(0,+∞)∪(-∞,-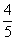 a)
D
a)
D
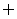
2 填空题
填空题
(1)不等式1≤|x-2|≤7的解集是
 答案:[-5,1]∪[3,9]
答案:[-5,1]∪[3,9]
(2)不等式 >a的解集是
>a的解集是  a=0时x>0;a>0时,0<x<
a=0时x>0;a>0时,0<x<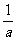 ;a<0时,x<
;a<0时,x<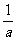 或x>0
或x>0
(3)不等式lg|x-4|<-1的解集是
 答案:{x|4<x<
答案:{x|4<x<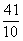 或
或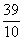 <x<4}
<x<4}
(4)不等式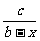 <a(a>0,b>0,c>0)的解集是
<a(a>0,b>0,c>0)的解集是  答案:{x|x<b或x>b-
答案:{x|x<b或x>b-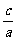 }
}
(5)若不等式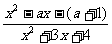 <0的解为-1<x<5,则a=
<0的解为-1<x<5,则a=  答案:4
答案:4
(6)不等式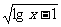 <3-lgx的解集是
<3-lgx的解集是  答案:10≤x<100
答案:10≤x<100
(7)函数f(x)=log2(x2-4),g(x)=2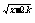 (k<-1),则f(x)g(x)的定义域为
(k<-1),则f(x)g(x)的定义域为  答案:[2k-2)∪(2,+∞)
答案:[2k-2)∪(2,+∞)
3 解下列不等式
解下列不等式
(1)(x+4)(x+5)2>(3x-2)(x+5)2;(2)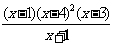 ≤0;(3)
≤0;(3)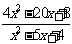 ≥3
≥3
解:(1)当x≠-5时,(x+5)2>0,两边同除以(x+5)2得x+4>3x-2,即x<3且x≠-5
∴x∈(-∞,-5)∪(-5,3)
(2)当x≠4时,原不等式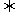 (x-1)(x-3)(x+1)≤0(x≠-1)
(x-1)(x-3)(x+1)≤0(x≠-1)  1≤x≤3或x<-1,当x=4时,显然左边=0,不等式成立
1≤x≤3或x<-1,当x=4时,显然左边=0,不等式成立
故原不等式的解集为{x|1≤x≤3或x<-1或x=4}
(3)原不等式可化为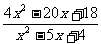 -3≥0
-3≥0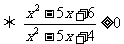
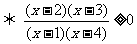 ∴x∈(-∞,1)∪[2,3]∪(4,+∞)
∴x∈(-∞,1)∪[2,3]∪(4,+∞)
4 设不等式(2x-1)>m(x2-1)对满足|m|≤2的一切实数m的值都成立,求x的取值范围
设不等式(2x-1)>m(x2-1)对满足|m|≤2的一切实数m的值都成立,求x的取值范围
解:①若x2-1=0,即x=±1,且2x-1>0,即x>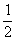 时,此时x=1,原不等式对|m|≤2恒成立;
时,此时x=1,原不等式对|m|≤2恒成立;
②若x2-1>0,要使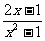 >m,对|m|≤2恒成立,只要
>m,对|m|≤2恒成立,只要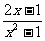 >2,即
>2,即
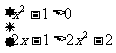 得1<x<
得1<x<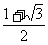

③若x2-1<0时,要使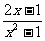 <m,对|m|≤2恒成立,只要
<m,对|m|≤2恒成立,只要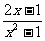 <-2,即
<-2,即
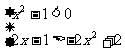 得
得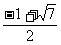 <x<1
<x<1
综合①②③得,所求x的范围为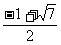 <x<
<x<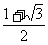

6.若方程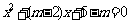 的两根都对于2,求实数m的范围
的两根都对于2,求实数m的范围 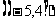
5.当a在什么范围内方程: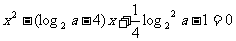 有两个不同的负根
有两个不同的负根 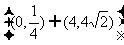
4.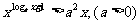
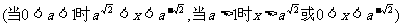
3.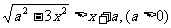

2. ,
,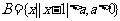 若
若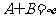 ,求a的取值范围
(a≥1)
,求a的取值范围
(a≥1)
1.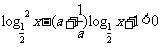
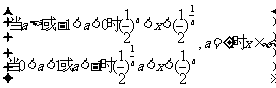
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com