
例1 解关于x的不等式

解:原不等式等价于  即
即 
∴
若a>1 , 
若0<a<1 , 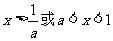
例2 解关于x的不等式 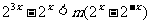
解:原不等式可化为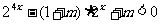 ,即
,即 
当m>1时,  ∴
∴
当m=1时,  ∴xÎφ
∴xÎφ
当0<m<1时,  ∴
∴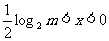
当m≤0时, x<0
例3 解关于x的不等式 
解:原不等式等价于 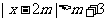
当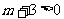 即
即 时,
时, 
∴
当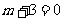 即
即 时,
时,  ∴x¹-6
∴x¹-6
当 即
即 时, xÎR
时, xÎR
例4 解关于x的不等式 
解:当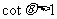 即qÎ(0,
即qÎ(0, )时,
)时,  ∴x>2或x<1
∴x>2或x<1
当 即q=
即q= 时, xÎφ
时, xÎφ
当 即qÎ(
即qÎ( ,
,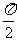 )时,
)时, 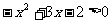 ∴1<x<2
∴1<x<2
例5 满足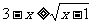 的x的集合为A;满足
的x的集合为A;满足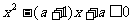 的x的集合为B
的x的集合为B 
1° 若AÌB 求a的取值范围;
2° 若AÊB 求a的取值范围;
3° 若A∩B为仅含一个元素的集合,求a的值
解:A=[1,2] , B={x|(x-a)(x-1)≤0}
当a≤1时, B=[a,1] 当a>1时 B=[1,a]
当a>2时, AÌB
当1≤a≤2时, AÊB
当a≤1时, A∩B仅含一个元素
例6 方程 有相异两实根,求a的取值范围
有相异两实根,求a的取值范围
解:原不等式可化为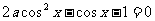
令  则
则 ,设
,设
又∵a>0 ∴

笔者认为,高考英语作文的主题越来越接近生活这是一个必然的趋势,这种趋势的目的是使考生将英语学习融入到生活中去,而不仅仅是脱离生活的、机械的学习,这也是应对中国学生在英语方面突出的“高分低能”的缺点的有效手段之一。
趋势2:英语作文的“语文化”
从上文中可以看出,高考英语作文这种从生活切入的主题似乎大大降低了其难度。但事实真的是这样吗?笔者对此持保留意见。虽然此类描述性的题目可以让学生更“有话可写”,可是我们必须注意到上述几乎所有的题目都有两个要求,描写只是其中的第一个要求,在我们看来那只是一个引子,仅仅是几句话带过的“述题”部分。而重头戏是后面的第二个要求,那才是评判作文质量的关键所在。还是以07年的高考为例,它要求在描写送出的礼物和所送的对象之后,还要写出该礼物对他(她)可能产生的影响或带来的变化。这就要求考生所描写的礼物对于接受礼物的人是有意义的,自然地,如果需要得到一个较高的分数,就要求考生在描写的背后揭示出具有一定深意的主题。再来看05年的高考,这次是要求以“天生我材必有用”为题。很明显,文章要求考生描写自己曾经做过的一件事情,从而证明人各有所长,无论才能大小都能成为有用的人。这就要求考生在选题上要花上一番心思,文章所描写的事情必须为文章的主题服务。尽量是一件小事,但是从这件小事上能够有“以小见大”的效果。所以说,虽然文章的主题和生活都是密切相关的,而且文章的素材也都是来源于生活的,可是考生在选题和文章的组织结构上必须多花些心思,这是不是同我们在处理高考中语文的作文题时的情形一样呢?
趋势3:及格容易,高分难
以前的英语作文,如果达到了要求的字数、基本无语法错误、思路清晰、表达及过渡流畅,一般达到这些要求,就能进入至少“中上”的档次。但是,描述性的文章不同于考生们平时常常接触到的议论文,它没有能够套用的固定模式,取而代之的是它对考生在文章结构的组织上提出更高的要求。因为一篇高考作文应该控制在120-150字之间,那么考生如何合理地安排呢?如果描述部分过多而忽略了中心的挖掘的话,那只能算是一篇“没有灵魂”的文章。因此,这里就要考验考生的概括和表达能力了,如何既做到“言简意赅”又能够表达清楚到位,这显然是比以前议论文一两句话的“述题”更为艰巨的任务。
另外,要想取得高分,还要求考生能够考虑那些别人想不到的主题。因为这里的描写可能会出现许许多多相近的表达,因此如果文章没有能够“脱颖而出”的地方,所得到的分数自然也比较普通。故要想取得高分,考生就要注重对于文章主题的挖掘,要让阅卷的老师看到你思想的光芒,发现你文章的闪光点。这些都是死板的模板、千篇一律的范文和单纯的描写所不能做到的。
23.已知函数f (x)=(x-1) , 数列{
, 数列{ }是公差为d的等差数列,数列{
}是公差为d的等差数列,数列{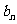 }是公比为q的等比数列(q∈R, q≠1, q≠0),
}是公比为q的等比数列(q∈R, q≠1, q≠0),
若 =f (d-1),
=f (d-1), 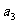 =f (d+1),
=f (d+1),  =f (q-1),
=f (q-1),  =f (q+1),
=f (q+1),
(1) 求数列{ }, {
}, {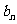 }的通项公式;
}的通项公式;
(2) 设数列{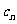 }对任意的自然数n均有
}对任意的自然数n均有
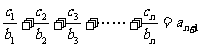 成立,求
成立,求 +
+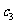 +
+ +……+
+……+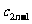 的值
的值
解:(1)  =f (d-1)=(d-2)
=f (d-1)=(d-2) ,
, 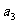 =f (d+1)=d
=f (d+1)=d ,
,
∴ 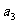 -
- =2d, 即d
=2d, 即d -(d-2)
-(d-2) =2d,
=2d,
解得d=2, ∴  =0,
=0,  =2(n-1),
=2(n-1),
又 =f (q-1)=(q-2)
=f (q-1)=(q-2) ,
,  =f (q+1)=q
=f (q+1)=q ,
,  =q
=q ,
,
∴  =q
=q ,
,
∵q ≠1, ∴ q=3, ∴ =1,
=1, 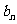 =3
=3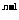
(2) 设 =
=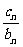 (n∈N), 数列{
(n∈N), 数列{ }的前n项和为
}的前n项和为 ,
,
则 =
= =2n,
=2n, 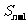 =
= =2(n-1),
=2(n-1),
∴ -
-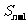 =2, 即
=2, 即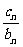 =2, ∴
=2, ∴ 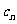 =2
=2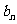 =2·3
=2·3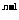
∴ +
+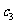 +
+ +……+
+……+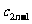
=2+2·3 +……+2·3
+……+2·3 =
=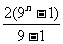 =
= ,
,
2.已知等差数列{ }的前n项和为
}的前n项和为 ,
,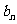 =
= , 且
, 且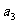
 =
=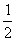 ,
, +
+ =21, (1) 求数列{bn}的通项公式;(2) 求证:
=21, (1) 求数列{bn}的通项公式;(2) 求证: +
+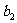 +
+ +……+
+……+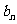 <2.
<2.
解:(1)设等差数列{ }的首项为
}的首项为 , 公差为d,则
, 公差为d,则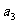
 =(
=( +2d)·
+2d)· =
=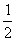 ,
,
 +
+ =8
=8 +13d=21, 解得
+13d=21, 解得  =1, d=1,
=1, d=1,
∴  =n,
=n,  =
=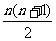 ,
, 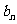 =
=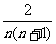 ;
;
(2)  +
+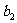 +
+ +……+
+……+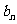
=2·[(1-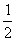 )+(
)+(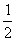 -
- )+……+(
)+……+( )]<2.
)]<2.
1.已知 , a
, a ,
, 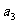 , …,
, …,  , …构成一等差数列,其前n项和为
, …构成一等差数列,其前n项和为 =n
=n , 设
, 设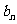 =
=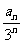 , 记{
, 记{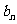 }的前n项和为
}的前n项和为 , (1) 求数列{
, (1) 求数列{ }的通项公式;(2) 证明:
}的通项公式;(2) 证明: <1.
<1.
解:(1)  =
=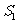 =1, 当n≥2时,
=1, 当n≥2时,  =
= -
-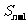 =2n-1;
=2n-1;
由于n=1时符合公式,∴  =2n-1 (n≥1).
=2n-1 (n≥1).
(2)  =
= ,
,
∴ 
 =
= ,
,
两式相减得

 =
= +
+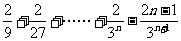 =
= +
+ (1-
(1- )-
)- ,
,
∴  =
=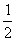 +
+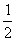 (1-
(1- )-
)- <1,
<1,
2.由1.得{ }是等比数列 a
}是等比数列 a =0.2 ,
q=
=0.2 ,
q=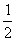
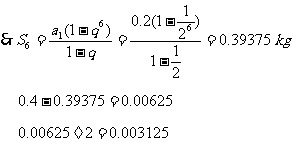
例3在等比数列 中,
中,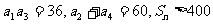 ,求
,求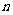 的范围
的范围
解:∵ ,∴
,∴
又∵ ,且
,且 ,∴
,∴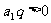 ,
,
∴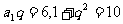 解之:
解之:
当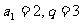 时,
时,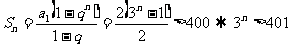 ,∴
,∴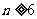
(∵
 )
)
当 时,
时, ,
,
∵ 且必须为偶数
且必须为偶数
∴ ,(∵
,(∵ )
)
例4 设{ }, {
}, {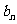 }都是等差数列,它们的前n项和分别为
}都是等差数列,它们的前n项和分别为 ,
,  , 已知
, 已知 ,求⑴
,求⑴ ;⑵
;⑵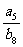
⑴ 解法1: =
=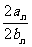 =
=
 =
=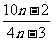 .
.
⑴解法2:∵{ }, {
}, {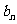 }都是等差数列
}都是等差数列
∴可设 =kn(5n+3),
=kn(5n+3),  =kn(2n-1)
=kn(2n-1)
∴ =
= -
-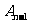 = k[n(5n+3)-(n-1)(5(n-1)+3)]=kn(10n-2),
= k[n(5n+3)-(n-1)(5(n-1)+3)]=kn(10n-2),
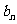 =
= -
- =k[n(2n-1)-(n-1)(2(n-1)-1)] =kn(4n-3),
=k[n(2n-1)-(n-1)(2(n-1)-1)] =kn(4n-3),
∴ =
= =
=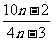
⑵解:由⑴解法2,有
 =
= -
-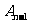 = k[n(5n+3)-(n-1)(5(n-1)+3)]=kn(10n-2),
= k[n(5n+3)-(n-1)(5(n-1)+3)]=kn(10n-2),
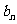 =
= -
- =k[n(2n-1)-(n-1)(2(n-1)-1)] =kn(4n-3),
=k[n(2n-1)-(n-1)(2(n-1)-1)] =kn(4n-3),
∴ =k
=k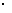 5
5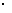 (10
(10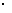 5-2)=240k
5-2)=240k
 =k
=k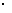 8
8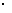 (4
(4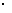 8-3)=232k
8-3)=232k
∴ 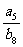 =
=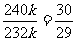
例5设等差数列{ }的前n项和为
}的前n项和为 ,
,
(1)
如果a =9, S
=9, S =40, 问是否存在常数c,使数列{
=40, 问是否存在常数c,使数列{ }成等差数列;
}成等差数列;
(2)
如果 =n
=n -6n, 问是否存在常数c,使得
-6n, 问是否存在常数c,使得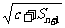 =
= 对任意自然数n都成立
对任意自然数n都成立
解:(1) 由a =9, S
=9, S =40, 得a
=40, 得a =7, d=2,
=7, d=2,
∴  =2n+5,
=2n+5,  =n2+6n,
=n2+6n,  =
=
∴ 当c=9时,  =n+3是等差数列;
=n+3是等差数列;
(2) 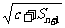 =
= 对任意自然数n都成立,
对任意自然数n都成立,
等价于{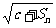 }成等差数列,
}成等差数列,
由于 =n
=n -6n
-6n
∴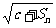 =
= ,
,
即使c=9, 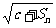 =|n-3|, 也不会成等差数列,
=|n-3|, 也不会成等差数列,
因此不存在这样的常数c使得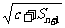 =
= 对任意自然数n都成立
对任意自然数n都成立
例1 在△ABC中,三边 成等差数列,
成等差数列, 也成等差数列,求证△ABC为正三角形
也成等差数列,求证△ABC为正三角形
证:由题设, 且
且
∴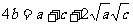
∴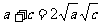 即
即  从而
从而
∴ (获证)
(获证)
例2 从盛有盐的质量分数为20%的盐水2 kg的容器中倒出1 kg盐水,然后加入1 kg水,以后每次都倒出1 kg盐水,然后再加入1 kg水,
问:1.第5次倒出的的1 kg盐水中含盐多少g?
2.经6次倒出后,一共倒出多少k盐?此时加1 kg水后容器内盐水的盐的质量分数为多少?
解:1.每次倒出的盐的质量所成的数列为{ },则:
},则:
a = 0.2 kg , a
= 0.2 kg , a =
=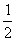 ×0.2 kg , a
×0.2 kg , a = (
= (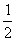 )
) ×0.2 kg
×0.2 kg
由此可见: = (
= (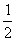 )
)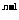 ×0.2 kg ,
×0.2 kg ,
 = (
= (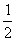 )
) ×0.2= (
×0.2= (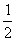 )
) ×0.2=0.0125 kg
×0.2=0.0125 kg
23. (金华卷,本题10分)
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y =  的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
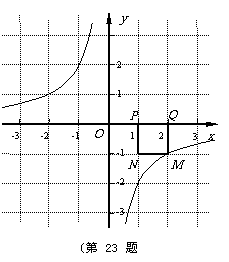 (1)如图所示,若反比例函数解析式为y=
(1)如图所示,若反比例函数解析式为y=  ,P点坐标为(1, 0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;
,P点坐标为(1, 0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;
(温馨提示:作图时,别忘
了用黑色字迹的钢笔或签字
笔描黑喔!)
M1的坐标是 ▲
(2) 请你通过改变P点坐标,对直线M1 M的解析式y﹦kx+b进行探究可得 k﹦ ▲ , 若点P的坐标为(m,0)时,则b﹦ ▲ ;
(3) 依据(2)的规律,如果点P的坐标为(6,0),请你求出点M1和点M的坐标.
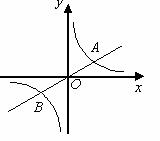
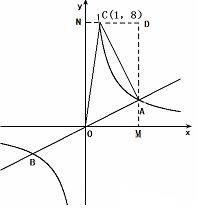
2.(2010年山东省济南市)如图,已知直线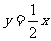 与双曲线
与双曲线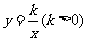 交于A,B两点,且点A的横坐标为4.
交于A,B两点,且点A的横坐标为4.
(1)求k的值;
(2)若双曲线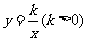 上一点C的纵坐标为8,求△AOC的面积;
上一点C的纵坐标为8,求△AOC的面积;
(3)过原点O的另一条直线l交双曲线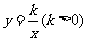 于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.
于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.
[关键词]反比例函数
[答案]
 (1)∵点A横坐标为4 ,
(1)∵点A横坐标为4 ,
∴当 x = 4时,y = 2
∴ 点A的坐标为(4,2 ) …………2’
∵点A是直线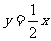 与双曲线
与双曲线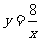 (k>0)的交点,
(k>0)的交点,
∴ k = 4×2 = 8 ………….3’
(2)解法一:
∵ 点C在双曲线 上,当y = 8时,x = 1
上,当y = 8时,x = 1
∴ 点C的坐标为(1,8)………..4’
过点A、C分别做x轴、y轴的垂线,垂足为M、N,得矩形DMON
S矩形ONDM= 32 , S△ONC = 4 , S△CDA = 9, S△OAM = 4
S△AOC= S矩形ONDM-S△ONC-S△CDA-S△OAM
 = 32-4-9-4 = 15 ………..6’
= 32-4-9-4 = 15 ………..6’
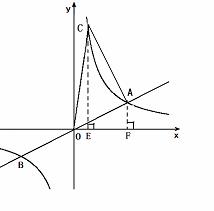
解法二:
过点 C、A分别做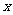 轴的垂线,垂足为E、F,
轴的垂线,垂足为E、F,
∵ 点C在双曲线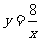 上,当y = 8时,x = 1。
上,当y = 8时,x = 1。
∴ 点C的坐标为(1,8)
∵ 点C、A都在双曲线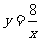 上,
上,
∴ S△COE = S△AOF = 4
∴ S△COE + S梯形CEFA = S△COA + S△AOF .
∴ S△COA = S梯形CEFA
∵ S梯形CEFA = ×(2+8)×3 = 15,
×(2+8)×3 = 15,
∴ S△COA = 15
(3)∵ 反比例函数图象是关于原点O的中心对称图形 ,
 ∴ OP=OQ,OA=OB
∴ OP=OQ,OA=OB
∴ 四边形APBQ是平行四边形
∴ S△POA =  S平行四边形APBQ =
S平行四边形APBQ = ×24 = 6
×24 = 6
设点P的横坐标为m(m > 0且 ),
),
得P(m, ) …………..7’
) …………..7’
过点P、A分别做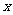 轴的垂线,垂足为E、F,
轴的垂线,垂足为E、F,
∵ 点P、A在双曲线上,∴S△POE = S△AOF = 4
若0<m<4,
∵ S△POE + S梯形PEFA = S△POA + S△AOF,
∴ S梯形PEFA = S△POA = 6
∴ 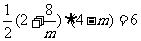
解得m= 2,m= - 8(舍去)
∴ P(2,4) ……………8’
若 m> 4,
 ∵ S△AOF+ S梯形AFEP = S△AOP + S△POE,
∵ S△AOF+ S梯形AFEP = S△AOP + S△POE,
∴ S梯形PEFA = S△POA = 6
∴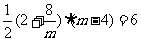 ,
,
解得m= 8,m =-2 (舍去)
∴ P(8,1)
∴ 点P的坐标是P(2,4)或P(8,1)………….9’
1. (2010年山东省济南市)若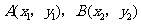 是双曲线
是双曲线 上的两点,且
上的两点,且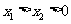 ,则
,则 {填“>”、“=”、“<”}.
{填“>”、“=”、“<”}.
[关键词]反比例函数
[答案]<
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com