
2.两个平面垂直的判定方法(判定方法有两种,一是利用定义,二是利用判定定理.)
1.两个平面垂直的定义、画法
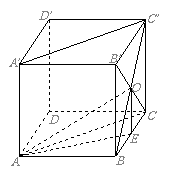
3.如图,正方体的棱长为1,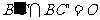 ,求:
,求:
(1)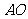 与
与 所成角;
所成角;
(2)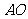 与平面
与平面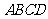 所成角的正切值;
所成角的正切值;
(3)平面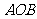 与平面
与平面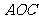 所成角
所成角
解:(1)∵ ∴
∴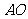 与
与 所成角就是
所成角就是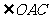
∵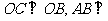 平面
平面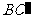 ∴
∴ (三垂线定理)
(三垂线定理)
在 中,
中,  ∴
∴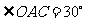
(2)作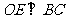 ,平面
,平面 平面
平面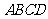
∴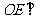 平面
平面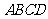 ,
,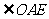 为
为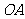 与平面
与平面 所成角
所成角
在 中,
中,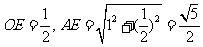 ∴
∴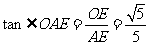
(3)∵ ∴
∴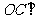 平面
平面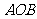
又∵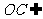 平面
平面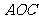 ∴平面
∴平面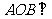 平面
平面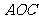
即平面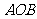 与平面
与平面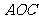 所成角为
所成角为

说明:本题包含了线线角,线面角和面面角三类问题,求角度问题主要是求两条异面直线所成角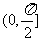 ,直线和平面所成角
,直线和平面所成角 ,二面角
,二面角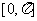 三种;求角度问题解题的一般步骤是:(1)找出这个角;(2)证明该角符合题意;(3)作出这个角所在的三角形,解三角形,求出角;求角度问题不论哪种情况都归结到两条直线所成角问题,即在线线成角中找到答案
三种;求角度问题解题的一般步骤是:(1)找出这个角;(2)证明该角符合题意;(3)作出这个角所在的三角形,解三角形,求出角;求角度问题不论哪种情况都归结到两条直线所成角问题,即在线线成角中找到答案
2.如果二面角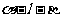 的平面角是锐角,点
的平面角是锐角,点 到
到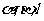 的距离分别为
的距离分别为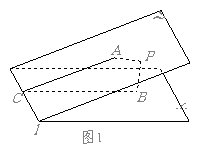
 ,求二面角的大小
,求二面角的大小
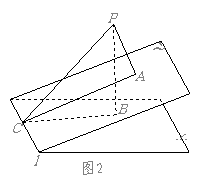
分析:点 可能在二面角
可能在二面角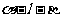 内部,也可能在外部,应区别处理
内部,也可能在外部,应区别处理
解:如图1是点 在二面角
在二面角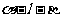 的内部时,图2是点
的内部时,图2是点 在二面角
在二面角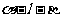 外部时,
外部时,
 ∵
∵ ∴
∴
∵ ∴面
∴面
同理,面
而面 面
面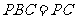
∴面 与面
与面 应重合
应重合
即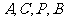 在同一平面内,
在同一平面内,
则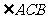 是二面角
是二面角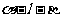 的平面角
的平面角
在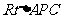 中,
中, ∴
∴
在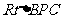 中,
中,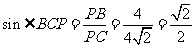 ∴
∴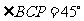
故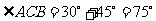 (图1)或
(图1)或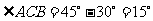 (图2)
(图2)
 即二面角
即二面角 的大小为
的大小为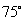 或
或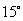

说明:作一个垂直于棱的平面,此平面与两个半平面的交线所成的角就是二面角的平面角
1.直角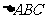 的斜边
的斜边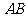 在平面
在平面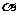 内,
内,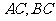 与
与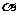 所成角分别为
所成角分别为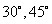 ,
, 是斜边
是斜边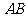 上的高线,求
上的高线,求 与平面
与平面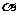 所成角的正弦值
所成角的正弦值
解:过点 作
作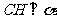 于点
于点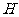 ,连接
,连接 ,
,
则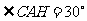 ,
,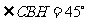 ,
,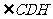 为所求
为所求 与
与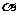 所成角,记为
所成角,记为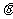 ,
,
 令
令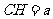 ,则
,则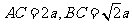 ,
,
则在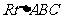 中,有
中,有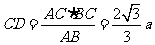
在 中,
中,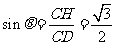
∴ 与平面
与平面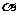 所成角的正弦值
所成角的正弦值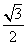 .
.
 例1
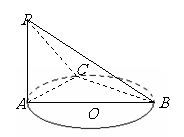
例1  如图,已知
如图,已知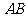 是圆
是圆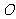 的直径,
的直径,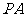 垂直于
垂直于 所在的平面,
所在的平面, 是圆周上不同于
是圆周上不同于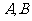 的任一点,求证:平面
的任一点,求证:平面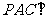 平面
平面 .
.
分析:根据“面面垂直”的判定定理,要证明两平面互相垂直,只要在其中一个平面中寻找一条与另一平面垂直的直线即可
解:∵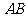 是圆
是圆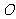 的直径,∴
的直径,∴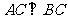 ,
,
又∵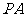 垂直于
垂直于 所在的平面,∴
所在的平面,∴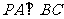 ,
,
∴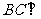 平面
平面 ,又
,又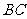 在平面
在平面 中,
中,
所以,平面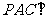 平面
平面 .
.
说明:由于平面 与平面
与平面 相交于
相交于 ,所以如果平面
,所以如果平面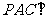 平面
平面 ,则在平面
,则在平面 中,垂直于
中,垂直于 的直线一定垂直于平面
的直线一定垂直于平面 ,这是寻找两个平面的垂线的常用方法
,这是寻找两个平面的垂线的常用方法
例2.已知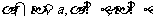 ,求证:
,求证: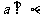 .
.
证明:设 ,
,
 在
在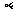 内取点
内取点 ,过
,过 作
作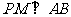 于
于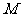 ,
,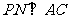 于点
于点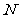 ,
,
∵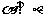 ,∴
,∴ ,
,
又∵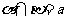 ,
,
∴ ,同理可得
,同理可得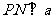 ,
,
∴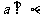 .
.
 例3.已知在一个
例3.已知在一个 的二面角的棱长有两点
的二面角的棱长有两点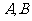 ,
, 分别是在这个二面角的两个平面内,且垂直于线段
分别是在这个二面角的两个平面内,且垂直于线段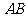 ,又知
,又知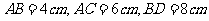 ,求
,求 的长
的长
解:由已知
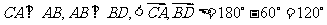 ,
,
∴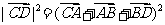
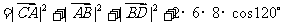
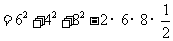
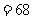 ,
,
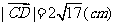
3.两平面垂直的性质定理: 若两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面
已知: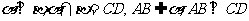 于点
于点 ,
,
求证: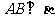 .(面面垂直
.(面面垂直 线面垂直)
线面垂直)
证明:在 内过
内过 作
作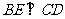 ,则由题意得
,则由题意得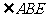 是
是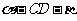 的平面角,
的平面角,
∵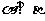 知
知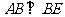 ,又∵
,又∵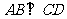 , ∴
, ∴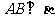 .
.
1  两个平面垂直的定义:
两个平面垂直的定义:
两个相交成直二面角的两个平面互相垂直;相交成直二面角的两个平面叫做互相垂直的平面
2.两平面垂直的判定定理: 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直
 已知:直线
已知:直线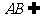 平面
平面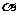 ,
,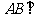 平面
平面 ,垂足为
,垂足为 ,
,
求证: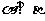 .(线面垂直
.(线面垂直 面面垂直)
面面垂直)
证明:如图所示,令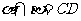 ,则
,则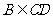 ,
,
 在
在 内过
内过 作
作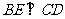 ,
,
∵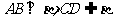 ,∴
,∴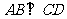 ,
,
∴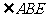 是二面角
是二面角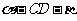 的平面角,
的平面角,
又∵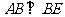 ,∴
,∴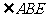 是直角,
是直角,
所以,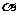 与
与 所成的二面角是直角,即
所成的二面角是直角,即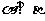 .
.
实例:建筑工地在砌墙时,常用铅垂的线来检查所砌的墙是否和水平面垂直
4.二面角的平面角:
(1)过二面角的棱上的一点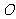 分别在两个半平面内作棱的两条垂线
分别在两个半平面内作棱的两条垂线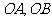 ,则
,则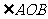 叫做二面角
叫做二面角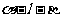 的平面角
的平面角
(2)一个平面垂直于二面角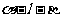 的棱
的棱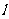 ,且与两半平面交线分别为
,且与两半平面交线分别为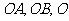 为垂足,则
为垂足,则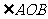 也是
也是 的平面角
的平面角
说明:(1)二面角的平面角范围是 ;
;
(2)二面角的平面角为直角时,则称为直二面角,组成直二面角的两个平面互相垂直
2. 公式:已知平面a的斜线a与a内一直线b相交成θ角,且a与a相交成j1角,a在a上的射影c与b相交成j2角,则有
公式:已知平面a的斜线a与a内一直线b相交成θ角,且a与a相交成j1角,a在a上的射影c与b相交成j2角,则有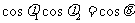
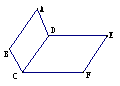
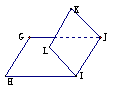
3  二面角的概念:平面内的一条直线把平面分为两个部分,其中的每一部分叫做半平面;从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面
二面角的概念:平面内的一条直线把平面分为两个部分,其中的每一部分叫做半平面;从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面 若棱为
若棱为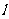 ,两个面分别为
,两个面分别为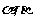 的二面角记为
的二面角记为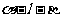 ;二面角的图形表示:
;二面角的图形表示:
第一种是卧式法,也称为平卧式:
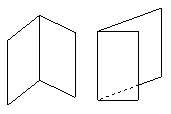
第二种是立式法,也称为直立式:

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com