5．下列各句句意明确，没有语病的一项是

A．高致病性禽流感是由高致病性禽流感病毒引起的鸡、鸭、鹅等禽类的烈性传染病。

B．通过在中国这几个月的生活，我已经把这一点感觉到了。

C．李丽最近这段时间可烦极了，周围的人谁也不搭理。

D．星期天，我们去郊游，山上那么多杜鹃，令我们游兴大发。

4．依次填入各句横线处的词语，最恰当的一组是

①作曲家多年积淀的质朴纯实与崇高宽阔的胸怀相　　 ，充满了纯朴的人性之美。

②他对我有很深的　　 ，以致在我提出合理的建议时也常常反对。

③这些赠品都是他们　 不舍得用，　　 不拿给人看，一直藏在小包袱的最里层的。

A．契合　 偏见　 素来　 从来　　 B．契合　 成见　 从来　 从来

C．吻合　 成见 　素来　 素来　　 D．吻合　 偏见　 从来　 从来

3．下列各句中，有错别字的一项是

A．因此他的呢帽的前沿压得比较低，脑袋总是微微地仰着。

B．金先生是个单身汉，无儿无女，但是过得自得其乐。

C．王府井人挤人，熙熙攘攘，谁也不会知道这位东张西望的老人是一位一肚子学问的大哲学家。

D．金先生晚年深居简出。他就和一个蹬平板三轮车的约好，每天蹬着他到王府井一带转一大圈。

2．下列各句中，标点符号使用有误的一项是

A．我给他画了几个青头菌、牛肝菌，一根大葱，两头蒜，还有一块很大的宣威火腿。——火腿是很少入画的。

B．联大有一次在龙云的长子，蒋介石的干儿子龙绳武家里开校友会，——龙云的长媳是清华校友，闻先生在会上大骂“蒋介石，王八蛋！混蛋！”

C．除了文学院大一学生必修逻辑，金先生还开了一门“符号逻辑”，是选修课。

D．林徽因死后，有一年，金先生在北京饭店请了一次客，老朋友收到通知，都纳闷：老金为什么请客？到了之后，金先生才宣布：“今天是徽因的生日。”

1．下列各句中加点熟语使用恰当的一句是

A．老师说，我是很喜欢“小女人”的文章的，至少它们不打肿脸充胖子，没有女强人的那种强悍和虚张声势。

B．他一再说今天上午有雨，果不其然，到了下午也没见到一个雨点。

C．他那些不经之谈即使说得天花乱坠也不会有人相信。

D．他为了写出反映农民精神面貌的文章，深入村庄，深居简出，获得第一手材料。

12．(2009年高考江苏卷)

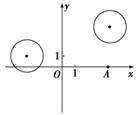
如图在平面直角坐标系xOy中，已知圆C₁：(x+3)²+(y－1)²＝4和圆C₂：(x－4)²+(y－5)²＝4.

(1)若直线l过点A(4,0)，且被圆C₁截得的弦长为2，求直线l的方程；

(2)设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线l₁和l₂，它们分别与圆C₁和C₂相交，且直线l₁被圆C₁截得的弦长与直线l₂被圆C₂截得的弦长相等，试求所有满足条件的点P的坐标．

解：(1)由于直线x＝4与圆C₁不相交，所以直线l的斜率存在．设直线l的方程为y＝k(x－4)，圆C₁的圆心到直线l的距离为d，因为直线l被圆C₁截得的弦长为2，所以d＝＝1.由点到直线的距离公式得d＝，从而k(24k+7)＝0，即k＝0或k＝－，所以直线l的方程为y＝0或7x+24y－28＝0.

(2)设点P(a，b)满足条件，不妨设直线l₁的方程为y－b＝k(x－a)，k≠0，则直线l₂的方程为y－b＝－(x－a)．因为圆C₁和圆C₂的半径相等，且直线l₁被圆C₁截得的弦长与直线l₂被圆C₂截得的弦长相等，所以圆C₁的圆心到直线l₁的距离和圆C₂的圆心到直线l₂的距离相等，即

＝，

整理得|1+3k+ak－b|＝|5k+4－a－bk|，从而1+3k+ak－b＝5k+4－a－bk或1+3k+ak－b＝－5k－4+a+bk，

即(a+b－2)·k＝b－a+3或(a－b+8)k＝a+b－5，因为k的取值有无穷多个，所以或解得或

这样点P只可能是点P₁(，－)或点P₂(－，)．

经检验点P₁和P₂满足题目条件．

11．(2010年江苏徐州调研)已知圆C的方程为x²+y²＝1，直线l₁过定点A(3,0)，且与圆C相切．

(1)求直线l₁的方程；

(2)设圆C与x轴交于P、Q两点，M是圆C上异于P、Q的任意一点，过点A且与x轴垂直的直线为l₂，直线PM交直线l₂于点P′，直线QM交直线l₂于点Q′.求证：以P′Q′为直径的圆C′总过定点，并求出定点坐标．

解：(1)∵直线l₁过点A(3,0)，且与圆C：x²+y²＝1相切，设直线l₁的方程为y＝k(x－3)，即kx－y－3k＝0，

则圆心O(0,0)到直线l₁的距离为d＝＝1，解得k＝±，

∴直线l₁的方程为y＝±(x－3)．

(2)对于圆C：x²+y²＝1，令y＝0，则x＝±1，即P(－1,0)，Q(1,0)．又直线l₂过点A且与x轴垂直，∴直线l₂方程为x＝3.

设M(s，t)，则直线PM的方程为y＝(x+1)．

解方程组得P′(3，)．同理可得Q′(3，)．

∴以P′Q′为直径的圆C′的方程为

(x－3)(x－3)+(y－)(y－)＝0，又s²+t²＝1，

∴整理得(x²+y²－6x+1)+y＝0，

若圆C′经过定点，只需令y＝0，从而有x²－6x+1＝0，解得x＝3±2，

∴圆C′总经过定点，定点坐标为(3±2，0)．

10．已知圆C₁：x²+y²+2x+2y－8＝0与圆C₂：x²+y²－2x+10y－24＝0相交于A、B两点，

(1)求公共弦AB所在的直线方程；

(2)求圆心在直线y＝－x上，且经过A、B两点的圆的方程．

解：(1)⇒x－2y+4＝0.

(2)由(1)得x＝2y－4，代入x²+y²+2x+2y－8＝0中得：y²－2y＝0.

∴或，即A(－4,0)，B(0,2)，

又圆心在直线y＝－x上，设圆心为M(x，－x)，则|MA|＝|MB|，解得M(－3,3)，∴⊙M：(x+3)²+(y－3)²＝10.

9．(2009年高考江西卷)设直线系M：xcosθ+(y－2)sinθ＝1(0≤θ≤2π)，对于下列四个命题：

A．存在一个圆与所有直线相交

B．存在一个圆与所有直线不相交

C．存在一个圆与所有直线相切

D．M中的直线所能围成的正三角形面积都相等

其中真命题的代号是________(写出所有真命题的代号)．

解析：xcosθ+ysinθ－2sinθ－1＝0.则点(0,2)到其直线的距离为

d＝＝1.

∴说明此直线是圆心为(0,2)，半径为1的圆的切线．

圆心为(0,2)，半径大于等于1的圆与所有直线相交，A对；

圆心为(0,2)，半径小于1的圆与所有直线不相交，B对；

圆心为(0,2)，半径等于1的圆与所有直线都相切，C对；

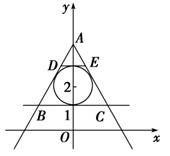
因为M中的直线与以(0,2)为圆心，半径为1的圆相切，所以M中的直线所能围成的正三角形面积不都相等．如图△ABC与△ADE均为等边三角形而面积不等．答案：A、B、C

8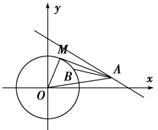．设圆O：x²+y²＝，直线l：x+3y－8＝0，点A∈l，使得圆O上存在点B，且∠OAB＝30°(O为坐标原点)，则点A的横坐标的取值范围是________．

解析：依题意点A∈l，设A(x₀，)．过点A作圆O的切线，切点为M，

则∠OAM≥∠OAB＝30°.从而sin∠OAM≥sin30°＝，即≥sin30°＝，就是|OA|²≤4(|OM|²)＝，x₀²+()²≤，5x₀²－8x₀≤0，解得x₀∈[0，]．

答案：[0，]