
5、在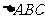 中,
中,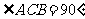 ,AB=8,
,AB=8,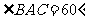 ,PC
,PC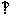 面ABC,PC=4,M是AB边上的一动点,则PM的最小值为( )
面ABC,PC=4,M是AB边上的一动点,则PM的最小值为( )
A、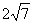 B、
B、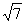 C、
C、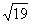 D、
D、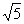
4、已知直线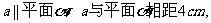 平面
平面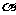 内直线b与c相距6cm且a||b,a与b相距5cm,则a、c相距( )
内直线b与c相距6cm且a||b,a与b相距5cm,则a、c相距( )
A、5cm
B、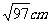 或5cm
C、
或5cm
C、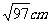 D 、
D 、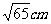 或5cm
或5cm
3、已知平面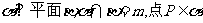 直线n过点P,则
直线n过点P,则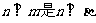 的( )
的( )
A、充分非必要条件 B、必要非充分条件 C、充要条件 D、非充分非必要条件
2、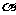 、
、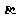 表示平面,
表示平面,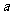 、
、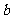 表示直线,则
表示直线,则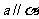 的一个充分条件是 ( )
的一个充分条件是 ( )

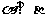 ,且
,且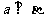
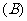
 ,且
,且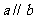

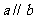 ,且
,且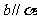
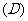
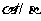 ,且
,且
1、已知直线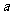 、
、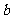 和平面
和平面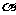 ,那么
,那么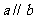 的一个必要不充分的条件是 ( )
的一个必要不充分的条件是 ( )

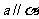 ,
,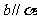
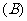
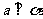 ,
,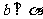

 且
且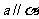
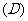
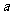 、
、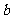 与
与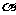 成等角
成等角
例1.如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
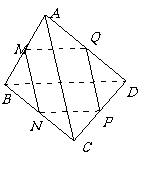 求证:(1)线段MP和NQ相交且互相平分;(2)AC∥平面MNP,BD∥平面MNP.
求证:(1)线段MP和NQ相交且互相平分;(2)AC∥平面MNP,BD∥平面MNP.
证明:(1) ∵M、N是AB、BC的中点,∴MN∥AC,MN=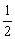 AC.
AC.
∵P、Q是CD、DA的中点,∴PQ∥CA,PQ=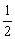 CA.
CA.
∴MN∥QP,MN=QP,MNPQ是平行四边形.
∴□MNPQ的对角线MP、NQ相交且互相平分.
(2)由(1),AC∥MN.记平面MNP(即平面MNPQ)为α.显然ACËα.
否则,若ACÌα,
由A∈α,M∈α,得B∈α;
由A∈α,Q∈α,得D∈α,则A、B、C、D∈α,
与已知四边形ABCD是空间四边形矛盾.
又∵MNÌα,∴AC∥α,
又AC Ëα,∴AC∥α,即AC∥平面MNP.
同理可证BD∥平面MNP.
例2.四面体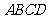 中,
中,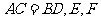 分别为
分别为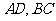 的中点,且
的中点,且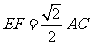 ,
,
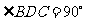 ,求证:
,求证: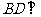 平面
平面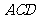
证明:取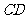 的中点
的中点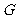 ,连结
,连结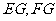 ,∵
,∵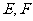 分别为
分别为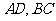 的中点,∴
的中点,∴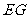
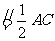
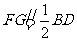 ,又
,又 ∴
∴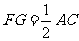 ,∴在
,∴在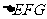 中,
中,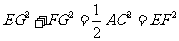
∴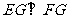 ,∴
,∴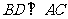 ,又
,又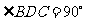 ,即
,即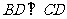 ,
,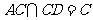
∴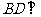 平面
平面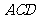
 例3. 如图,直三棱柱
例3. 如图,直三棱柱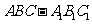 中,
中,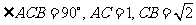 ,侧棱
,侧棱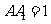 ,侧面
,侧面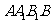 的两条对角线交于点
的两条对角线交于点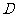 ,
,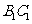 的中点为
的中点为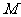 ,求证:
,求证: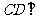 平面
平面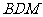
证明:连结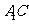 ,∵
,∵ ∴
∴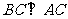 ,在直三棱柱
,在直三棱柱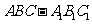 中
中
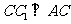 ,∴
,∴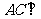 平面
平面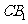 ,∵
,∵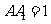 ,
,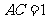
∴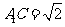 ,∴
,∴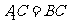 ,∵
,∵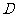 是侧面
是侧面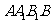 的两条对角
的两条对角
线的交点,∴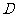 是
是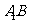 与
与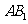 的中点,∴
的中点,∴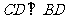 ,连结
,连结
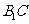 ,取
,取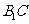 的中点
的中点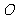 ,连结
,连结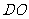 ,则
,则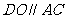 ,
,
∵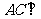 平面
平面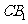 ,∴
,∴ 平面
平面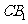 ,∴
,∴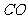 是
是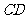 在
在
平面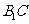 内的射影。在
内的射影。在 中,
中,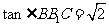
在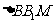 中,
中,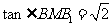 ,∴
,∴
∴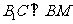 ,∴
,∴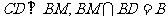 ,∴
,∴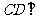 平面
平面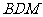
例4.如图,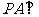 矩形
矩形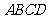 所在的平面,
所在的平面,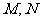 分别是
分别是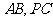 的中点,
的中点,
(1)求证: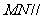 平面
平面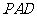 ;
(2)求证:
;
(2)求证: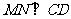
 (3)若
(3)若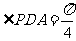 ,求证:
,求证: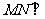 平面
平面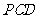
4.设三棱锥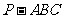 的顶点
的顶点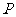 在平面
在平面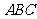 上的射影是
上的射影是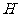 ,给出以下命题:
,给出以下命题:
①若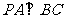 ,
,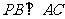 ,则
,则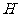 是
是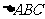 的垂心
的垂心
②若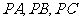 两两互相垂直,则
两两互相垂直,则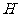 是
是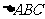 的垂心
的垂心
③若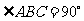 ,
,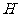 是
是 的中点,则
的中点,则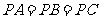
④若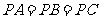 ,则
,则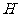 是
是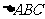 的外心
的外心
其中正确命题的命题是 ①②③④
3.在直四棱柱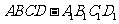 中,当底面四边形
中,当底面四边形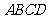 满足条件
满足条件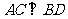 时,
时,
有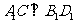 (注:填上你认为正确的一种条件即可,不必考虑所有可能的情况)
(注:填上你认为正确的一种条件即可,不必考虑所有可能的情况)
2.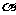 、
、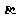 表示平面,
表示平面,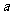 、
、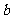 表示直线,则
表示直线,则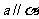 的一个充分条件是 (
的一个充分条件是 (
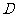 )
)

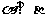 ,且
,且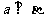
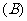
 ,且
,且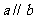

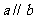 ,且
,且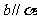
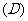
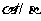 ,且
,且
1.已知直线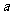 、
、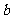 和平面
和平面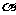 ,那么
,那么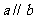 的一个必要不充分的条件是 (
的一个必要不充分的条件是 ( 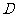 )
)

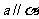 ,
,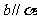
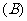
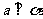 ,
,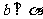

 且
且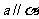
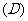
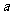 、
、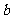 与
与 成等角
成等角
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com