14．设二次函数f(x)＝ax²+bx+c(a>0)，方程f(x)－x＝0的两个根x₁、x₂满足0<x₁<x₂<.

(1)当x∈(0，x₁)时，证明x<f(x)<x₁.

(2)设函数f(x)的图象关于直线x＝x₀对称，证明：x₀<.

解：(1)令F(x)＝f(x)－x，因为x₁，x₂是方程f(x)－x＝0的根，∴F(x)＝a(x－x₁)(x－x₂)，当x∈(0，x₁)时

∵x₁<x₂得(x－x₁)(x－x₂)>0又a>0得

F(x)＝a(x－x₁)(x－x₂)>0即x<f(x)

x₁－f(x)＝x₁－a(x－x₁)(x－x₂)－x＝(x₁－x)[1+a(x－x₂)]

∵x₁－x>0,1+a(x－x₂)＝1+ax－ax₂>1－ax₂>0

∴x₁－f(x)>0，∴f(x)<x₁，∴x<f(x)<x₁

(2)依题意知x₀＝－，∵x₁，x₂是方程f(x)－x＝0的根，即x₁，x₂是方程ax²+(b－1)x+c＝0的根

∴x₁+x₂＝－，x₀＝－＝＝

∵ax₂<1，∴x₀<＝

13．已知函数f(x)＝ax²+4(a为非零实数)，设函数F(x)＝.

(1)若f(－2)＝0，求F(x)的表达式；

(2)在(1)的条件下，解不等式1≤|F(x)|≤2；

(3)设mn<0，m+n>0，试判断F(m)+F(n)能否大于0?

解：(1)∵f(－2)＝0，∴4a+4＝0，得a＝－1，

∴f(x)＝－x²+4，

∴F(x)＝.

(2)∵|F(－x)|＝|F(x)|，∴|F(x)|是偶函数，故可以先求x>0的情况，当x>0时，由|F(2)|＝0，故当0<x≤2时，解不等式1≤－x²+4≤2，得≤x≤；当x>2时，解不等式1≤x²－4≤2，得≤x≤；

同理，当x<0时，可解得－≤x≤－或－≤x≤－.

综上所述，原不等式的解为：

≤x≤或≤x≤或－≤x≤－或－≤x≤－.

(3)∵f(x)＝ax²+4，

∴F(x)＝，

∵mn<0，不妨设m>0，则n<0，

又m+n>0，∴m>－n>0，∴m²>n²，

∴当a>0时，F(m)+F(n)能大于0，

当a<0时，F(m)+F(n)不能大于0.

12．(2009·江苏卷)设a为实数，函数f(x)＝2x²+(x－a)|x－a|.

(Ⅰ)若f(0)≥1，求a的取值范围；

(Ⅱ)求f(x)的最小值；

(Ⅲ)设函数h(x)＝f(x)，x∈(a，+∞)，直接写出(不需给出演算步骤)不等式h(x)≥1的解集．

分析：本小题主要考查函数的概念、性质、图象及解一元二次不等式等基础知识，考查灵活运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力．

解：(Ⅰ)因为f(0)＝－a|－a|≥1，所以－a>0，即a<0.

由a²≥1知a≤－1.

因此，a的取值范围为(－∞，－1]．

(Ⅱ)记f(x)的最小值为g(a)．我们有

f(x)＝2x²+(x－a)|x－a|

＝

(ⅰ)当a≥0时，f(－a)＝－2a²，

由①②知f(x)≥－2a²，此时g(a)＝－2a².

(ⅱ)当a<0时，f()＝a².

若x>a，则由①知f(x)≥a²；若x≤a，

则x+a≤2a<0，由②知f(x)≥2a²>a².

此时g(a)＝a².

综上得g(a)＝

(Ⅲ)ⅰ当a∈(－∞，－]∪[，+∞)时，解集为(a，+∞)；

(ⅱ)当a∈[－，)时，解集为[，+∞)；

(ⅲ)当a∈(－，－)时，解集为

(a，]∪[，+∞)．

11．(2008·浙江)已知t为常数，函数y＝|x²－2x－t|在区间[0,3]上的最大值为2，则t＝________.

答案：1

解析：令m＝x²－2x∈[－1,3]，y＝|m－t|的最大值在m＝－1或m＝3时取得，|－m－1|²－|3－m|²＝8(t－1)，当t≥1时，y_max＝|t+1|＝t+1＝2，∴t＝1.

当t<1时，y_max＝|3－t|＝3－t＝2，t＝1(舍去)，综合分析得t＝1故填1.

10．设x、y是关于m的方程m²－2am+a+b＝0的两个实根，则(x－1)²+(y－1)²的最小值是________．

答案：8

解析：由Δ＝(－2a)²－4(a+b)≥0得a≤－2或a≥3于是有(x－1)²+(y－1)²＝x²+y²－2(x+y)+2＝(x+y)²－2xy－2(x+y)+2＝(2a)²－2(a+b)－4a+2＝4a²－6a－10＝4(a－)²－.

由此可知，当a＝3时，(x－1)²+(y－1)²取得最小值8.

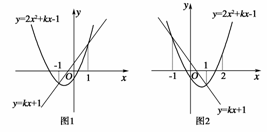
9．(2008·上海十二校二模)已知f(x)＝|x²－1|+x²+kx，若关于x的方程f(x)＝0在(0,2)上有两个解x₁，x₂，则k的取值范围是________．

答案：

解析：f(x)＝|x²－1|+x²+kx

＝

当k≥0时，函数的图象如图1，显然不合题意，当k<0时，函数的图象如图2，设g(x)＝2x²+kx－1，h(x)＝kx+1，由题意知

解得－<k<－1，综上所述，关于x的方程f(x)＝0在(0,2)上有两个解x₁，x₂，则k的取值范围是，故填.

8．(2008·华南师大附中)设b>0，二次函数y＝ax²+bx+a²－1的图象为如下图之一，则a的值为(　)

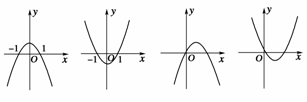
A．1　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B．－1

C.　 　　　　　　　　　　　　　　　　　　　　　　 D.

答案：B

解析：前两个图象的对称轴－＝0，b＝0，不合题意；由后两个图象知－>0，且f(0)＝a²－1＝0，求得a＝－1，故选B.

7．设f(x)是定义在R上的奇函数，且当x≥0时f(x)＝x²，若对任意的x∈[t，t+2]不等式f(x+t)≥2f(x)恒成立，则实数t的取值范围是(　)

A．[，+∞)　 　　　　　　　　　　　　　　　　　　 B．[2，+∞)

C．(0,2]　 　　　　　　　　　　　　　　　　　　　　　　　　 D．[－，－1]∪[，]

答案：A

解析：当t＝时，≤x≤2+，f(x+)－2f(x)＝(x+)²－2x²＝2+2x－x²≥2+2(2+)²－(2+)²＝0.即t＝时不等式成立．

当t＝2时，2≤x≤4，f(x+2)－2f(x)＝(x+2)²－2x²＝4+4x－x²≥4+4×4－4²>0.∴t＝2时不等式成立，所以选A.

6．已知f(x)＝1－(x－a)(x－b)，并且m，n是方程f(x)＝0的两根，则实数a，b，m，n的大小关系可能是(　)

A．m<a<b<n　 　　　　　　　　　　　　　　　　　　　　 B．a<m<n<b

C．a<m<b<n 　　　　　　　　　　　　　　　　　　　　　 D．m<a<n<b

答案：A

解析：方程f(x)＝0，m、n可看作f(x)与x轴交点的横坐标，a、b可看作g(x)＝－(x－a)(x－b)与x轴交点的横坐标．

所以a，b，m，n可以排列成m<a<b<n的形式，故选A.

5．(2008·成都市第一次检测题)已知函数y＝f(x)＝x²－2x－3与y＝－3在同一平面直角坐标系中的图象如右图所示．记F(x)为“f(|x|)”与“－3”中较小的一个，则下列关于函数y＝F(x)的说法中，正确的是(　)

A．F(4)<F(－5)

B．F(－1)是函数y＝F(x)的一个极小值

C．方程F(x)＝0有两个实数根

D．y＝F(x)在(－∞，1)上单调递增

答案：B

解析：在图形中勾画出y＝F(x)的图象，易知选B.