32.(2009福建卷文)(本小题满分12分)21世纪教育网 
已知函数
其中
，
(I)若
求
的值；
(Ⅱ)在(I)的条件下，若函数
的图像的相邻两条对称轴之间的距离等于
，求函数的解析式；并求最小正实数
，使得函数的图像象左平移个单位所对应的函数是偶函数。
解法一：
(I)由
得
即
又
21世纪教育网
(Ⅱ)由(I)得，
依题意，
又
故
函数的图像向左平移个单位后所对应的函数为
是偶函数当且仅当
即
从而，最小正实数
解法二：
(I)同解法一
(Ⅱ)由(I)得，
依题意， 21世纪教育网
又
，故
函数的图像向左平移个单位后所对应的函数为
是偶函数当且仅当
对
恒成立
亦即
对恒成立。
即
对恒成立。
故
21世纪教育网
从而，最小正实数
31.(2009四川卷理)(本小题满分12分)
在
中，
为锐角，角
所对应的边分别为
，且
(I)求
的值；
(II)若
，求的值。
本小题主要考查同角三角函数间的关系，两角和差的三角函数、二倍角公式、正弦定理等基础知识及基本运算能力。
解：(Ⅰ)
、
为锐角，
，
又，21世纪教育网
，
，
…………………………………………6分
(Ⅱ)由(Ⅰ)知,
. 21世纪教育网
由正弦定理
得
，即
，
，
，
……………………………………12分
30.(2009天津卷理)(本小题满分12分)
在⊿ABC中，BC=
，AC=3，sinC=2sinA
(I) 求AB的值：
(II) 求sin
的值 21世纪教育网
本小题主要考查正弦定理、余弦定理、同角三角函数的基本关系、二倍角的正弦与余弦、两角差的正弦等基础知识，考查基本运算能力。满分12分。
(Ⅰ)解：在△ABC中，根据正弦定理，
于是AB=
(Ⅱ)解：在△ABC中，根据余弦定理，得cosA=
于是
sinA=
从而sin2A=2sinAcosA=
,cos2A=cos2A-sin2A=
21世纪教育网
所以
sin(2A-
)=sin2Acos-cos2Asin=
29.(2009湖南卷理)(本小题满分12分)21世纪教育网
在，已知
，求角A，B，C的大小。
解：设
由
得
，所以
又
因此
由
得
，于是
所以，
，因此
，既
由A=知
，所以
，
，从而
或
，既或
故
或
。
28.(2009宁夏海南卷文)(本小题满分12分)
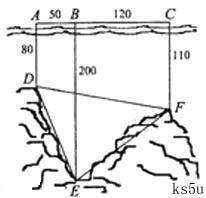如图，为了解某海域海底构造，在海平面内一条直线上的A，B，C三点进行测量，已知
，
，于A处测得水深
，于B处测得水深，于C处测得水深，求∠DEF的余弦值。
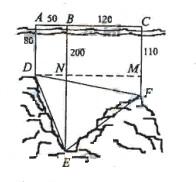
(17) 解：
作交BE于N，交CF于M．21世纪教育网
，
，
． ．．．．．．6分
在
中，由余弦定理，
. ．．．．．．12分
27.(2009湖北卷文)(本小题满分12分)
在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且
(Ⅰ)确定角C的大小：
(Ⅱ)若c＝
,且△ABC的面积为
,求a+b的值。
解(1)由
及正弦定理得，
21世纪教育网
是锐角三角形，
(2)解法1：
由面积公式得
由余弦定理得21世纪教育网
由②变形得
解法2：前同解法1，联立①、②得
消去b并整理得
解得
所以
故
21世纪教育网
26.(2009四川卷文)(本小题满分12分)
在中，为锐角，角
所对的边分别为
，且
(I)求的值；
(II)若，求的值。21世纪教育网
[解析](I)∵为锐角，
∴ 
∵ 
∴ 
…………………………………………6分
(II)由(I)知，∴
由得
，即
又∵ 21世纪教育网
∴ 
∴ 
∴ 
…………………………………………12分
17、解(1)由最低点为
得A=2.
由x轴上相邻的两个交点之间的距离为得=，即
，
由点在图像上的
故
21世纪教育网
又
(2)
当
=，即
时，取得最大值2；当
即时，取得最小值-1，故的值域为[-1,2] 21世纪教育网
25.(2009陕西卷理)(本小题满分12分)
已知函数
(其中
)的图象与x轴的交点中，相邻两个交点之间的距离为，且图象上一个最低点为.
(Ⅰ)求的解析式；(Ⅱ)当
，求的值域.
24.(2009陕西卷文)(本小题满分12分)
已知函数(其中)的周期为
，且图象上一个最低点为.
(Ⅰ)求的解析式；(Ⅱ)当
，求的最值.
解析:(1)由最低点为 由
由点在图像上得
即
所以故
又
，所以
所以
(Ⅱ)因为
所以当
时，即x=0时，f(x)取得最小值1；
；
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com