
18.(2009湖北卷理)(本小题满分14分)(注意:在试题卷上作答无效)
过抛物线 的对称轴上一点
的对称轴上一点 的直线与抛物线相交于M、N两点,自M、N向直线
的直线与抛物线相交于M、N两点,自M、N向直线 作垂线,垂足分别为
作垂线,垂足分别为 、
、 。
。 

(Ⅰ)当 时,求证:
时,求证: ⊥
⊥ ;
;
(Ⅱ)记
 、
、 、
、 的面积分别为
的面积分别为 、
、 、
、 ,是否存在
,是否存在 ,使得对任意的
,使得对任意的 ,都有
,都有 成立。若存在,求出
成立。若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。
20题。本小题主要考察抛物线的定义和几何性质等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力。(14分)
解:依题意,可设直线MN的方程为 ,则有21世纪教育网
,则有21世纪教育网 


由 消去x可得
消去x可得


从而有 ①
①
于是 ②
②
又由 ,
, 可得
可得 ③
③
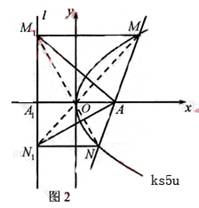
(Ⅰ)如图1,当 时,点
时,点 即为抛物线的焦点,
即为抛物线的焦点, 为其准线
为其准线
此时 ①可得
①可得
证法1:
 21世纪教育网
21世纪教育网 

证法2:




(Ⅱ)存在 ,使得对任意的
,使得对任意的 ,都有
,都有 成立,证明如下:
成立,证明如下:
证法1:记直线 与x轴的交点为
与x轴的交点为 ,则
,则 。于是有
。于是有




将①、②、③代入上式化简可得

上式恒成立,即对任意 成立
成立 

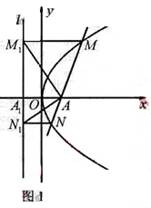
证法2:如图2,连接 ,则由
,则由 可得
可得
 ,所以直线
,所以直线 经过原点O,
经过原点O,
同理可证直线 也经过原点O
也经过原点O
又 设
设 则
则

17.(2009天津卷文)(本小题满分14分)
已知椭圆 (
( )的两个焦点分别为
)的两个焦点分别为 ,过点
,过点 的直线与椭圆相交于点A,B两点,且
的直线与椭圆相交于点A,B两点,且
(Ⅰ求椭圆的离心率
(Ⅱ)直线AB的斜率;
(Ⅲ)设点C与点A关于坐标原点对称,直线 上有一点H(m,n)(
上有一点H(m,n)( )在
)在 的外接圆上,求
的外接圆上,求 的值。
的值。
[答案](1) (2)
(2) (3)
(3)
[解析]
(1)解:由 ,得
,得 ,从而
,从而
 ,整理得
,整理得 ,故离心率
,故离心率
(2)解:由(1)知, ,所以椭圆的方程可以写为
,所以椭圆的方程可以写为
设直线AB的方程为 即
即
由已知设 则它们的坐标满足方程组
则它们的坐标满足方程组 21世纪教育网
21世纪教育网 

消去y整理,得
依题意,
而 ,有题设知,点B为线段AE的中点,所以
,有题设知,点B为线段AE的中点,所以
联立三式,解得 ,将结果代入韦达定理中解得
,将结果代入韦达定理中解得
(3)由(2)知, ,当
,当 时,得A
时,得A 由已知得
由已知得
线段 的垂直平分线l的方程为
的垂直平分线l的方程为 直线l与x轴的交点
直线l与x轴的交点 是
是 的外接圆的圆心,因此外接圆的方程为
的外接圆的圆心,因此外接圆的方程为
直线 的方程为
的方程为 ,于是点
,于是点 满足方程组
满足方程组 由
由 ,解得
,解得 ,故
,故
当 时,同理可得
时,同理可得
[考点定位]本小题主要考查椭圆的标准方程和几何性质,直线方程,圆的方程等基础知识。考查用代数方法研究圆锥曲线的性质和数形结合的思想,考查运算能力和推理能力。
16.(2009江西卷理)(本小题满分12分)
 已知点
已知点 为双曲线
为双曲线 (
( 为正常数)上任一点,
为正常数)上任一点, 为双曲线的右焦点,过
为双曲线的右焦点,过 作右准线的垂线,垂足为
作右准线的垂线,垂足为 ,连接
,连接 并延长交
并延长交 轴于
轴于 . 21世纪教育网
. 21世纪教育网 

(1) 求线段
 的中点
的中点 的轨迹
的轨迹 的方程;
的方程;
(2) 设轨迹 与
与 轴交于
轴交于 两点,在
两点,在 上任取一点
上任取一点 ,直线
,直线 分别交
分别交 轴于
轴于 两点.求证:以
两点.求证:以 为直径的圆过两定点.
为直径的圆过两定点.
解: (1) 由已知得 ,则直线
,则直线 的方程为:
的方程为: ,
,
令 得
得 ,即
,即 ,
,
设 ,则
,则 ,即
,即 代入
代入 得:
得: ,
,
即 的轨迹
的轨迹 的方程为
的方程为 . 21世纪教育网
. 21世纪教育网 

(2) 在 中令
中令 得
得 ,则不妨设
,则不妨设 ,
,
于是直线 的方程为:
的方程为: ,
, 直线
直线 的方程为:
的方程为: ,
,
则 ,
,
则以 为直径的圆的方程为:
为直径的圆的方程为: 
 ,
,
令 得:
得: ,而
,而 在
在 上,则
上,则 ,
,
于是 ,即以
,即以 为直径的圆过两定点
为直径的圆过两定点 .
.
15.(2009江西卷文)(本小题满分14分)
 如图,已知圆
如图,已知圆
 是椭圆
是椭圆 的内接△
的内接△ 的内切圆, 其中
的内切圆, 其中 为椭圆的左顶点.
为椭圆的左顶点.
(1)求圆 的半径
的半径 ;
;
(2)过点 作圆
作圆 的两条切线交椭圆于
的两条切线交椭圆于 两点,
两点,
|
|
 与圆
与圆 相切.
相切.
解: (1)设
 ,过圆心
,过圆心 作
作 于
于 ,
, 交长轴于
交长轴于
由 得
得 ,
,
即  (1)
(1)
而点
 在椭圆上,
在椭圆上, (2)
(2)
由(1)、 (2)式得 ,解得
,解得 或
或 (舍去)
(舍去)
(2) 设过点 与圆
与圆 相切的直线方程为:
相切的直线方程为: (3)
(3)
则 ,即
,即 (4)
(4)
解得
将(3)代入 得
得 ,则异于零的解为
,则异于零的解为
设 ,
, ,则
,则
则直线 的斜率为:
的斜率为:
于是直线 的方程为:
的方程为:
即
则圆心 到直线
到直线 的距离
的距离 21世纪教育网
21世纪教育网 

故结论成立.
14.(2009安徽卷文)(本小题满分12分)
已知椭圆 (a>b>0)的离心率为
(a>b>0)的离心率为 ,以原点为圆心。椭圆短半轴长半径的
,以原点为圆心。椭圆短半轴长半径的
圆与直线y=x+2相切,
(Ⅰ)求a与b;21世纪教育网 

(Ⅱ)设该椭圆的左,右焦点分别为 和
和 ,直线
,直线 过
过 且与x轴垂直,动直线
且与x轴垂直,动直线 与y轴垂直,
与y轴垂直, 交
交 与点p..求线段P
与点p..求线段P 垂直平分线与
垂直平分线与 的交点M的轨迹方程,并指明曲线类型。
的交点M的轨迹方程,并指明曲线类型。
[思路](1)由椭圆 建立a、b等量关系,再根据直线与椭圆相切求出a、b.
建立a、b等量关系,再根据直线与椭圆相切求出a、b.
(2)依据几何关系转化为代数方程可求得,这之中的消参就很重要了。
[解析](1)由于 ∴
∴ ∴
∴ 又
又 ∴b2=2,a2=3因此,
∴b2=2,a2=3因此, . 21世纪教育网
. 21世纪教育网 

(2)由(1)知F1,F2两点分别为(-1,0),(1,0),由题意可设P(1,t).(t≠0).那么线段PF1中点为 ,设M(x、y)是所求轨迹上的任意点.由于
,设M(x、y)是所求轨迹上的任意点.由于 则
则 消去参数t得
消去参数t得
,其轨迹为抛物线(除原点)
13.(2009安徽卷理)(本小题满分13分)21世纪教育网 

点 在椭圆
在椭圆 上,
上, 直线
直线 与直线
与直线 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为 ,直线
,直线 的倾斜角为
的倾斜角为 .
.
(I)证明: 点 是椭圆
是椭圆 与直线
与直线 的唯一交点;
的唯一交点; 

(II)证明: 构成等比数列.
构成等比数列.
解:本小题主要考查直线和椭圆的标准方程和参数方程,直线和曲线的几何性质,等比数列等基础知识。考查综合运用知识分析问题、解决问题的能力。本小题满分13分。
解:(I)(方法一)由 得
得 代入椭圆
代入椭圆 ,
,
得 .
.
将 代入上式,得
代入上式,得 从而
从而
因此,方程组 有唯一解
有唯一解 ,即直线
,即直线 与椭圆有唯一交点P.
与椭圆有唯一交点P. 

(方法二)显然P是椭圆与 的交点,若Q
的交点,若Q 是椭圆与
是椭圆与 的交点,代入
的交点,代入 的方程
的方程 ,得
,得
即 故P与Q重合。
故P与Q重合。
(方法三)在第一象限内,由 可得
可得
椭圆在点P处的切线斜率
切线方程为 即
即 。
。
因此, 就是椭圆在点P处的切线。21世纪教育网
就是椭圆在点P处的切线。21世纪教育网 

根据椭圆切线的性质,P是椭圆与直线 的唯一交点。
的唯一交点。
(II)
 的斜率为
的斜率为
 的斜率为
的斜率为
由此得
 构成等比数列。
构成等比数列。
12.(2009广东卷理)(本小题满分14分)
已知曲线 与直线
与直线 交于两点
交于两点 和
和 ,且
,且 .记曲线
.记曲线 在点
在点 和点
和点 之间那一段
之间那一段 与线段
与线段 所围成的平面区域(含边界)为
所围成的平面区域(含边界)为 .设点
.设点 是
是 上的任一点,且点
上的任一点,且点 与点
与点 和点
和点 均不重合.
均不重合.
(1)若点 是线段
是线段 的中点,试求线段
的中点,试求线段 的中点
的中点 的轨迹方程;
的轨迹方程;
(2)若曲线 与
与 有公共点,试求
有公共点,试求 的最小值.
的最小值.
解:(1)联立 与
与 得
得 ,则
,则 中点
中点 ,设线段
,设线段 的中点
的中点 坐标为
坐标为 ,则
,则 ,即
,即 ,又点
,又点 在曲线
在曲线 上,
上,
∴ 化简可得
化简可得 ,又点
,又点 是
是 上的任一点,且不与点
上的任一点,且不与点 和点
和点 重合,则
重合,则 ,即
,即 ,∴中点
,∴中点 的轨迹方程为
的轨迹方程为 (
( ).
).

 21世纪教育网
21世纪教育网


(2)曲线 ,
,
即圆 :
: ,其圆心坐标为
,其圆心坐标为 ,半径
,半径
由图可知,当 时,曲线
时,曲线 与点
与点 有公共点;
有公共点;
当 时,要使曲线
时,要使曲线 与点
与点 有公共点,只需圆心
有公共点,只需圆心 到直线
到直线 的距离
的距离 ,得
,得 ,则
,则 的最小值为
的最小值为 .
.
11.(2009全国卷Ⅱ文)(本小题满分12分)
|


|

(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有 成立?
成立?
若存在,求出所有的P的坐标与l的方程;若不存在,说明理由。
解析:本题考查解析几何与平面向量知识综合运用能力,第一问直接运用点到直线的距离公式以及椭圆有关关系式计算,第二问利用向量坐标关系及方程的思想,借助根与系数关系解决问题,注意特殊情况的处理。
解:(Ⅰ)设 当
当 的斜率为1时,其方程为
的斜率为1时,其方程为 到
到 的距离为
的距离为

故  ,
,  21世纪教育网
21世纪教育网 

由 
得  ,
, =
=
(Ⅱ)C上存在点 ,使得当
,使得当 绕
绕 转到某一位置时,有
转到某一位置时,有 成立。
成立。
由 (Ⅰ)知C的方程为 +
+ =6.
设
=6.
设
(ⅰ) 
C  成立的充要条件是
成立的充要条件是 , 且
, 且
整理得 

故  ①
①
将

 21世纪教育网
21世纪教育网 

于是
 ,
,  =
= ,
,

代入①解得, ,此时
,此时
于是 =
= ,
即
,
即 21世纪教育网
21世纪教育网 

因此, 当 时,
时, ,
,
 ;
;
当 时,
时, ,
,
 。
。
(ⅱ)当 垂直于
垂直于 轴时,由
轴时,由 知,C上不存在点P使
知,C上不存在点P使 成立。
成立。
综上,C上存在点 使
使 成立,此时
成立,此时 的方程为
的方程为
 .
.
10.(2009江苏卷)(本小题满分16分)
 在平面直角坐标系
在平面直角坐标系 中,已知圆
中,已知圆 和圆
和圆 .
.
(1)若直线 过点
过点 ,且被圆
,且被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线 的方程;
的方程;
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线 和
和 ,它们分别与圆
,它们分别与圆 和圆
和圆 相交,且直线
相交,且直线 被圆
被圆 截得的弦长与直线
截得的弦长与直线 被圆
被圆 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
[解析] 本小题主要考查直线与圆的方程、点到直线的距离公式,考查数学运算求解能力、综合分析问题的能力。满分16分。
(1)设直线 的方程为:
的方程为: ,即
,即
由垂径定理,得:圆心 到直线
到直线 的距离
的距离 ,
,
结合点到直线距离公式,得:

化简得:
求直线 的方程为:
的方程为: 或
或 ,即
,即 或
或
(2) 设点P坐标为 ,直线
,直线 、
、 的方程分别为:21世纪教育网
的方程分别为:21世纪教育网 

 ,即:
,即:
因为直线 被圆
被圆 截得的弦长与直线
截得的弦长与直线 被圆
被圆 截得的弦长相等,两圆半径相等。由垂径定理,得::圆心
截得的弦长相等,两圆半径相等。由垂径定理,得::圆心 到直线
到直线 与
与 直线
直线 的距离相等。
的距离相等。

故有: ,
,
化简得:
关于 的方程有无穷多解,有:
的方程有无穷多解,有:
 21世纪教育网
21世纪教育网 

解之得:点P坐标为 或
或 。
。
9. (2009山东卷文)(本小题满分14分)
设 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量 ,向量
,向量 ,
, ,动点
,动点 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状; 21世纪教育网 

(2)已知 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
(3)已知 ,设直线
,设直线 与圆C:
与圆C: (1<R<2)相切于A1,且
(1<R<2)相切于A1,且 与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
解:(1)因为 ,
, ,
, ,
,
所以 , 即
, 即 . 21世纪教育网
. 21世纪教育网 

当m=0时,方程表示两直线,方程为 ;
;
当 时, 方程表示的是圆
时, 方程表示的是圆
当 且
且 时,方程表示的是椭圆;
时,方程表示的是椭圆;
当 时,方程表示的是双曲线.
时,方程表示的是双曲线.
(2).当 时, 轨迹E的方程为
时, 轨迹E的方程为 ,设圆心在原点的圆的一条切线为
,设圆心在原点的圆的一条切线为 ,解方程组
,解方程组 得
得 ,即
,即 ,
,
要使切线与轨迹E恒有两个交点A,B,
则使△= ,
,
即 ,即
,即 , 且
, 且
 ,
,
要使 , 需使
, 需使 ,即
,即 ,
,
所以 , 即
, 即 且
且 , 即
, 即 恒成立.
恒成立.
所以又因为直线 为圆心在原点的圆的一条切线,
为圆心在原点的圆的一条切线,
所以圆的半径为 ,
, ,
所求的圆为
,
所求的圆为 .
.
当切线的斜率不存在时,切线为 ,与
,与 交于点
交于点 或
或 也满足
也满足 .
.
综上, 存在圆心在原点的圆 ,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 .
.
(3)当 时,轨迹E的方程为
时,轨迹E的方程为 ,设直线
,设直线 的方程为
的方程为 ,因为直线
,因为直线 与圆C:
与圆C: (1<R<2)相切于A1,
由(2)知
(1<R<2)相切于A1,
由(2)知 , 即
, 即 ①,
①,
因为 与轨迹E只有一个公共点B1,
与轨迹E只有一个公共点B1,
由(2)知 得
得 ,
,
即 有唯一解
有唯一解
则△= ,
即
,
即 , ②
, ②
由①②得 , 此时A,B重合为B1(x1,y1)点, 21世纪教育网
, 此时A,B重合为B1(x1,y1)点, 21世纪教育网 

由 中
中 ,所以,
,所以, ,
,
B1(x1,y1)点在椭圆上,所以 ,所以
,所以 ,
,
在直角三角形OA1B1中, 因为
因为 当且仅当
当且仅当 时取等号,所以
时取等号,所以 ,即
,即
当 时|A1B1|取得最大值,最大值为1.
时|A1B1|取得最大值,最大值为1.
[命题立意]:本题主要考查了直线与圆的方程和位置关系,以及直线与椭圆的位置关系,可以通过解方程组法研究有没有交点问题,有几个交点的问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com