
8.(2009山东卷理)(本小题满分14分)
设椭圆E:  (a,b>0)过M(2,
(a,b>0)过M(2, ) ,N(
) ,N( ,1)两点,O为坐标原点,
,1)两点,O为坐标原点,
(I)求椭圆E的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
解:(1)因为椭圆E:  (a,b>0)过M(2,
(a,b>0)过M(2, ) ,N(
) ,N( ,1)两点,
,1)两点,
所以 解得
解得 所以
所以 椭圆E的方程为
椭圆E的方程为
(2)假设存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 ,设该圆的切线方程为
,设该圆的切线方程为 解方程组
解方程组 得
得 ,即
,即 , 21世纪教育网
, 21世纪教育网 

则△= ,即
,即
 ,
, 要使
要使 ,需使
,需使 ,即
,即 ,所以
,所以 ,所以
,所以 又
又 ,所以
,所以 ,所以
,所以 ,即
,即 或
或 ,因为直线
,因为直线 为圆心在原点的圆的一条切线,所以圆的半径为
为圆心在原点的圆的一条切线,所以圆的半径为 ,
, ,
, ,所求的圆为
,所求的圆为 ,此时圆的切线
,此时圆的切线 都满足
都满足 或
或 ,而当切线的斜率不存在时切线为
,而当切线的斜率不存在时切线为 与椭圆
与椭圆 的两个交点为
的两个交点为 或
或 满足
满足 ,综上, 存在圆心在原点的圆
,综上, 存在圆心在原点的圆 ,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 .
.
因为 ,
,
所以 ,
,

 ,
,
①当 时
时
因为 所以
所以 ,
,
所以 ,
,
所以 当且仅当
当且仅当 时取”=”. 21世纪教育网
时取”=”. 21世纪教育网 

② 当 时,
时, .
.
③ 当AB的斜率不存在时, 两个交点为 或
或 ,所以此时
,所以此时 ,
,
综上, |AB |的取值范围为 即:
即: 
[命题立意]:本题属于探究是否存在的问题,主要考查了椭圆的标准方程的确定,直线与椭圆的位置关系直线与圆的位置关系和待定系数法求方程的方法,能够运用解方程组法研究有关参数问题以及方程的根与系数关系.
7.(2009江苏卷)(本题满分10分)
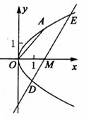
 在平面直角坐标系
在平面直角坐标系 中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在
中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在 轴上。
轴上。
(1)求抛物线C的标准方程;
(2)求过点F,且与直线OA垂直的直线的方程;
(3)设过点 的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为
的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为 ,求
,求 关于
关于 的表达式。
的表达式。
[解析] [必做题]本小题主要考查直线、抛物线及两点间的距离公式等基本知识,考查运算求解能力。满分10分。


6.(2009北京理)(本小题共14分)
已知双曲线 的离心率为
的离心率为 ,右准线方程为
,右准线方程为
(Ⅰ)求双曲线 的方程;
的方程;
(Ⅱ)设直线 是圆
是圆 上动点
上动点 处的切线,
处的切线, 与双曲线
与双曲线 交
交
于不同的两点 ,证明
,证明 的大小为定值.
的大小为定值.
[解法1]本题主要考查双曲线的标准方程、圆的切线方程等基础知识,考查曲线和方程
的关系等解析几何的基本思想方法,考查推理、运算能力.
(Ⅰ)由题意,得 ,解得
,解得 ,
,
∴ ,∴所求双曲线
,∴所求双曲线 的方程为
的方程为 .
.
(Ⅱ)点 在圆
在圆 上,
上,
圆在点 处的切线方程为
处的切线方程为 ,
,
化简得 .
.
由 及
及 得
得 ,
,
∵切线 与双曲线C交于不同的两点A、B,且
与双曲线C交于不同的两点A、B,且 ,
,
∴ ,且
,且 ,
,
设A、B两点的坐标分别为 ,
,
则 ,
,
∵ ,且
,且
 ,
,


 .
.
∴  的大小为
的大小为 .
.
[解法2](Ⅰ)同解法1.
(Ⅱ)点 在圆
在圆 上,
上,
圆在点 处的切线方程为
处的切线方程为 ,
,
化简得 .由
.由 及
及 得
得
 ①
①
 ②
②
∵切线 与双曲线C交于不同的两点A、B,且
与双曲线C交于不同的两点A、B,且 ,
,
∴ ,设A、B两点的坐标分别为
,设A、B两点的坐标分别为 ,
,
则 ,
,
∴ ,∴
,∴
 的大小为
的大小为 .
.
(∵ 且
且 ,∴
,∴ ,从而当
,从而当 时,方程①和方程②的判别式均大于零).
时,方程①和方程②的判别式均大于零).
5.(2009北京文)(本小题共14分)21世纪教育网 

已知双曲线 的离心率为
的离心率为 ,右准线方程为
,右准线方程为 。
。
(Ⅰ)求双曲线C的方程;
(Ⅱ)已知直线 与双曲线C交于不同的两点A,B,且线段AB的中点在圆
与双曲线C交于不同的两点A,B,且线段AB的中点在圆 上,求m的值.
上,求m的值.
[解析]本题主要考查双曲线的标准方程、圆的切线方程等基础知识,考查曲线和方程
的关系等解析几何的基本思想方法,考查推理、运算能力.
(Ⅰ)由题意,得 ,解得
,解得 ,
,
∴ ,∴所求双曲线
,∴所求双曲线 的方程为
的方程为 .
.
(Ⅱ)设A、B两点的坐标分别为 ,线段AB的中点为
,线段AB的中点为 ,
,
由 得
得 (判别式
(判别式 ),
),
∴ ,
,
∵点 在圆
在圆 上,
上,
∴ ,∴
,∴ .
.
4.(2009浙江文)(本题满分15分)已知抛物线 :
: 上一点
上一点 到其焦点的距离为
到其焦点的距离为 .
.
(I)求 与
与 的值;
的值;
(II)设抛物线 上一点
上一点 的横坐标为
的横坐标为 ,过
,过 的直线交
的直线交 于另一点
于另一点 ,交
,交 轴于点
轴于点 ,过点
,过点 作
作 的垂线交
的垂线交 于另一点
于另一点 .若
.若 是
是 的切线,求
的切线,求 的最小值.
的最小值.
解析(Ⅰ)由抛物线方程得其准线方程: ,根据抛物线定义
,根据抛物线定义
点 到焦点的距离等于它到准线的距离,即
到焦点的距离等于它到准线的距离,即 ,解得
,解得
 抛物线方程为:
抛物线方程为: ,将
,将 代入抛物线方程,解得
代入抛物线方程,解得
(Ⅱ)由题意知,过点 的直线
的直线 斜率存在且不为0,设其为
斜率存在且不为0,设其为 。
。
则 ,当
,当 则
则 。
。
联立方程 ,整理得:
,整理得:
即: ,解得
,解得 或
或
 ,而
,而 ,
, 直线
直线 斜率为
斜率为 21世纪教育网
21世纪教育网 

 ,联立方程
,联立方程
整理得: ,即:
,即:
 ,解得:
,解得: ,或
,或
 ,
,
而抛物线在点N处切线斜率:
 MN是抛物线的切线,
MN是抛物线的切线, , 整理得
, 整理得
 ,解得
,解得 (舍去),或
(舍去),或 ,
,
3.(2009浙江理)(本题满分15分)已知椭圆 :
: 的右顶点为
的右顶点为 ,过
,过 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为 .
.
(I)求椭圆 的方程;
的方程;
(II)设点 在抛物线
在抛物线 :
: 上,
上, 在点
在点 处
处
的切线与 交于点
交于点 .当线段
.当线段 的中点与
的中点与 的中
的中
点的横坐标相等时,求 的最小值.
的最小值.
解析:(I)由题意得 所求的椭圆方程为
所求的椭圆方程为 ,21世纪教育网
,21世纪教育网 

(II)不妨设 则抛物线
则抛物线 在点P处的切线斜率为
在点P处的切线斜率为 ,直线MN的方程为
,直线MN的方程为 ,将上式代入椭圆
,将上式代入椭圆 的方程中,得
的方程中,得 ,即
,即 ,因为直线MN与椭圆
,因为直线MN与椭圆 有两个不同的交点,所以有
有两个不同的交点,所以有 ,
,
设线段MN的中点的横坐标是 ,则
,则 ,21世纪教育网
,21世纪教育网 

设线段PA的中点的横坐标是 ,则
,则 ,由题意得
,由题意得 ,即有
,即有 ,其中的
,其中的 或
或 ;
;
当 时有
时有 ,因此不等式
,因此不等式 不成立;因此
不成立;因此 ,当
,当 时代入方程
时代入方程 得
得 ,将
,将 代入不等式
代入不等式 成立,因此
成立,因此 的最小值为1.
的最小值为1.
2.(2009全国卷Ⅰ理)(本小题满分12分)(注意:在试题卷上作答无效)
如图,已知抛物线 与圆
与圆 相交于
相交于 、
、 、
、 、
、 四个点。
四个点。
(I)求 得取值范围;
得取值范围;
(II)当四边形 的面积最大时,求对角线
的面积最大时,求对角线 、
、 的交点
的交点 坐标
坐标
分析:(I)这一问学生易下手。将抛物线 与圆
与圆 的方程联立,消去
的方程联立,消去 ,整理得
,整理得 .............(*)
.............(*)
抛物线 与圆
与圆 相交于
相交于 、
、 、
、 、
、 四个点的充要条件是:方程(*)有两个不相等的正根即可.易得
四个点的充要条件是:方程(*)有两个不相等的正根即可.易得 .考生利用数形结合及函数和方程的思想来处理也可以.
.考生利用数形结合及函数和方程的思想来处理也可以.
(II)考纲中明确提出不考查求两个圆锥曲线的交点的坐标。因此利用设而不求、整体代入的 方法处理本小题是一个较好的切入点.
设四个交点的坐标分别为 、
、 、
、 、
、 。
。
则由(I)根据韦达定理有 ,
,
则

令 ,则
,则 下面求
下面求 的最大值。
的最大值。
方法一:利用三次均值求解。三次均值目前在两纲中虽不要求,但在处理一些最值问题有时很方便。它的主要手段是配凑系数或常数,但要注意取等号的条件,这和二次均值类似。


当且仅当 ,即
,即 时取最大值。经检验此时
时取最大值。经检验此时 满足题意。
满足题意。
方法二:利用求导处理,这是命题人的意图。具体解法略。
下面来处理点 的坐标。设点
的坐标。设点 的坐标为:
的坐标为:
由 三点共线,则
三点共线,则 得
得 。
。
以下略。
1.(2009年广东卷文)(本小题满分14分)
已知椭圆G的中心在坐标原点,长轴在 轴上,离心率为
轴上,离心率为 ,两个焦点分别为
,两个焦点分别为 和
和 ,椭圆G上一点到
,椭圆G上一点到 和
和 的距离之和为12.圆
的距离之和为12.圆 :
:
 的圆心为点
的圆心为点 .
.
(1)求椭圆G的方程
(2)求 的面积
的面积
(3)问是否存在圆 包围椭圆G?请说明理由.
包围椭圆G?请说明理由.
[解析](1)设椭圆G的方程为: (
( )半焦距为c;
)半焦距为c;
则 , 解得
, 解得 ,
, 
所求椭圆G的方程为: . 21世纪教育网
. 21世纪教育网 

(2 )点 的坐标为
的坐标为

(3)若 ,由
,由 可知点(6,0)在圆
可知点(6,0)在圆 外,
外,
若 ,由
,由 可知点(-6,0)在圆
可知点(-6,0)在圆 外;
外;
 不论K为何值圆
不论K为何值圆 都不能包围椭圆G.
都不能包围椭圆G.
23.(2009上海卷文)已知 是椭圆
是椭圆 的两个焦点,
的两个焦点, 为椭圆
为椭圆 上的一点,且
上的一点,且 。若
。若 的面积为9,则
的面积为9,则 .
.
[答案]3
[解析]依题意,有 ,可得4c2+36=4a2,即a2-c2=9,故有b=3。
,可得4c2+36=4a2,即a2-c2=9,故有b=3。
22.(2009年上海卷理)已知 、
、 是椭圆
是椭圆 (
( >
> >0)的两个焦点,
>0)的两个焦点, 为椭圆
为椭圆 上一点,且
上一点,且 .若
.若 的面积为9,则
的面积为9,则 =____________.
=____________. 

[答案]3
[解析]依题意,有 ,可得4c2+36=4a2,即a2-c2=9,故有b=3。
,可得4c2+36=4a2,即a2-c2=9,故有b=3。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com