
20.(2009全国卷Ⅱ理)已知双曲线 的右焦点为
的右焦点为 ,过
,过 且斜率为
且斜率为 的直线交
的直线交 于
于 两点,若
两点,若 ,则
,则 的离心率为w.w.w.k.s.5.u.c.o.
的离心率为w.w.w.k.s.5.u.c.o.
 m A.
m A. B.
B.  C.
C.  D.
D. 
解:设双曲线 的右准线为
的右准线为 ,过
,过 分 别作
分 别作 于
于 ,
, 于
于 ,
,  ,由直线AB的斜率为
,由直线AB的斜率为 ,知直线AB的倾斜角为
,知直线AB的倾斜角为 ,
,
由双曲线的第二定义有
 .
.
又 故选A
故选A
19.(2009全国卷Ⅱ理)已知直线 与抛物线
与抛物线 相交于
相交于 两点,
两点, 为
为 的焦点,若
的焦点,若 ,则
,则
A.
 B.
B. C.
C.
 D.
D. 
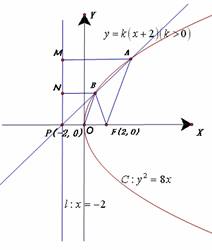
解:设抛物线 的准线为
的准线为 直线
直线  恒过定点P
恒过定点P .如图过
.如图过 分 别作
分 别作 于
于 ,
, 于
于 , 由
, 由 ,则
,则 ,点B为AP的中点.连结
,点B为AP的中点.连结 ,则
,则 ,
,  点
点 的横坐标为
的横坐标为 , 故点
, 故点 的坐标为
的坐标为 , 故选D
, 故选D
18.(2009四川卷文)已知双曲线 的左、右焦点分别是
的左、右焦点分别是 、
、 ,其一条渐近线方程为
,其一条渐近线方程为 ,点
,点
 在双曲线上.则
在双曲线上.则 ·
· =
=
A. -12 B. -2 C. 0 D. 4
[答案]C
[解析]由渐近线方程为 知双曲线是等轴双曲线,∴双曲线方程是
知双曲线是等轴双曲线,∴双曲线方程是 ,于是两焦点坐标分别是(-2,0)和(2,0),且
,于是两焦点坐标分别是(-2,0)和(2,0),且 或
或 .不妨去
.不妨去 ,则
,则 ,
,
 .∴
.∴ ·
· =
=
17.(2009湖北卷理)已知双曲线 的准线过椭圆
的准线过椭圆 的焦点,则直线
的焦点,则直线 与椭圆至多有一个交点的充要条件是
与椭圆至多有一个交点的充要条件是
A.  B.
B. 
C.  D.
D.

[答案]A
[解析]易得准线方程是
所以 即
即 所以方程是
所以方程是
联立 可得
可得 由
由 可解得A
可解得A
16.(2009天津卷文)设双曲线 的虚轴长为2,焦距为
的虚轴长为2,焦距为 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A  B
B  C
C  D
D
[答案]C
[解析]由已知得到 ,因为双曲线的焦点在x轴上,故渐近线方程为
,因为双曲线的焦点在x轴上,故渐近线方程为
[考点定位]本试题主要考查了双曲线的几何性质和运用。考察了同学们的运算能力和推理能力。
15.(2009江西卷理)过椭圆 (
( )的左焦点
)的左焦点 作
作 轴的垂线交椭圆于点
轴的垂线交椭圆于点 ,
, 为右焦点,若
为右焦点,若 ,则椭圆的离心率为
,则椭圆的离心率为
A. B.
B. C.
C. D.
D. 21世纪教育网
21世纪教育网 

答案:B
[解析]因为 ,再由
,再由 有
有 从而可得
从而可得 ,故选B
,故选B
14.(2009江西卷文)设 和
和 为双曲线
为双曲线 (
( )的两个焦点, 若
)的两个焦点, 若 ,
, 是正三角形的三个顶点,则双曲线的离心率为
是正三角形的三个顶点,则双曲线的离心率为
A. B.
B. C.
C. D.3
D.3
答案:B
[解析]由 有
有 ,则
,则 ,故选B.
,故选B.
13.(2009安徽卷文)直线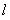 过点(-1,2)且与直线垂直,则
过点(-1,2)且与直线垂直,则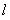 的方程是
的方程是
A.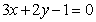 B.
B.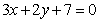
C.  D.
D.
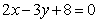
[解析]可得 斜率为
斜率为 即
即 ,选A。
,选A。
[答案]A
12.(2009安徽卷文)下列曲线中离心率为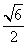 的是21世纪教育网
的是21世纪教育网 

A.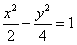 B.
B.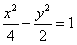 C.
C. D.
D.
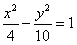
[解析]依据双曲线 的离心率
的离心率 可判断得.
可判断得. .选B。
.选B。
[答案]B
11.(2009安徽卷理)下列曲线中离心率为 的是
的是
(A) (B)
(B) (C)
(C) (D)
(D)
[解析]由 得
得 ,选B
,选B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com