
22. (本题满分8分)已知数列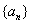 满足
满足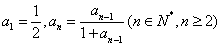 .
.
(Ⅰ)求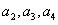 ,并猜想数列
,并猜想数列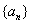 的通项公式;
的通项公式;
(Ⅱ)令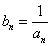 且
且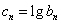 ,判断数列
,判断数列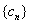 是否为等比数列?并说明理由.
是否为等比数列?并说明理由.
21.(本题满分6分)设命题 :曲线
:曲线 上任一点处的切线的倾斜角都是锐角;命题
上任一点处的切线的倾斜角都是锐角;命题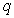 :直线
:直线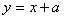 与曲线
与曲线 有两个不同的公共点. 若命题
有两个不同的公共点. 若命题 和命题
和命题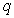 中有且只有一个是真命题,求实数
中有且只有一个是真命题,求实数 的取值范围.
的取值范围.
20. 若在圆内作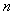 条弦,两两相交,将圆最多分割成
条弦,两两相交,将圆最多分割成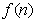 部分,有
部分,有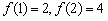 ,则
,则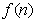 的表达式为 ▲ .
的表达式为 ▲ .
19. 已知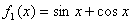 ,记
,记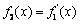 ,
,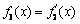 ,…,
,…,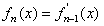
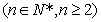 ,则
,则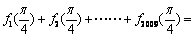 ▲ .
▲ .
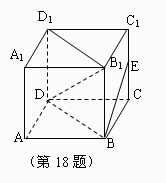
18.如图,在正方体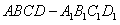 中,
中,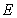 是
是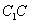 中点,
中点,
则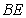 与平面
与平面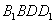 所成角的正弦值为 ▲ .
所成角的正弦值为 ▲ .
17. 设向量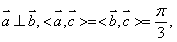 且
且
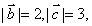 则
则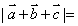 ▲ .
▲ .
16.已知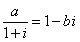 (其中
(其中 、
、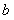 是实数,
是实数,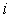 是虚数单位),则
是虚数单位),则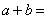 ▲ .
▲ .
15.在抛物线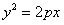 上,横坐标为
上,横坐标为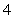 的点到焦点的距离为
的点到焦点的距离为 ,则
,则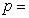 ▲ .
▲ .
14. 已知点 是双曲线
是双曲线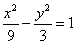 右支上的任意一点,由
右支上的任意一点,由 点向双曲线的两条渐近线引垂线,垂足为
点向双曲线的两条渐近线引垂线,垂足为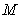 和
和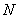 ,则
,则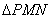 的面积为
的面积为
A.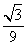 B.
B.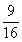 C.
C.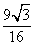 D.
D.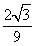
13. 设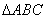 是边长为
是边长为 的等边三角形,
的等边三角形, 是
是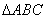 内任意一点,
内任意一点, 到三边的距离分别为
到三边的距离分别为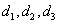 ,根据三角形
,根据三角形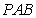 、
、 、
、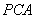 的面积之和等于
的面积之和等于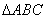 的面积,可得
的面积,可得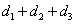 为定值
为定值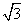 ,由此类比:
,由此类比: 是棱长为3的正四面体
是棱长为3的正四面体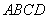 内任意一点,且
内任意一点,且 到各面的距离分别为
到各面的距离分别为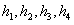 ,则
,则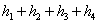 的值为
的值为
A.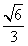 B.
B.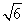 C.
C.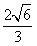 D.
D. 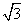
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com