
11.(2009安徽卷文)(本小题满分12分)
某良种培育基地正在培育一种小麦新品种A,将其与原有的一个优良品种B进行对照
试验,两种小麦各种植了25亩,所得亩产数据(单位:千克)如下:. 

品种A:357,359,367,368,375,388,392,399,400,405,414,
415,421,423,423,427,430,430,434,443,445,451,454
品种B:363,371,374,383,385,386,391,392,394,395,397
397,400,401,401,403,406,407,410,412,415,416,422,430
(Ⅰ)完成所附的茎叶图
(Ⅱ)用茎叶图处理现有的数据,有什么优点?. 

(Ⅲ)通过观察茎叶图,对品种A与B的亩产量及其稳定性进行比较,写出统计结论。
[思路]由统计知识可求出A、B两种品种的小麦稳定性大小并画出茎叶图,用茎叶图处理数据,看其分布就比较明了。. 

[解析](1)茎叶图如图所示
|
A |
|
B |
|
9 7 |
35 |
|
|
8 7 |
36 |
3 |
|
5 |
37 |
1 4 |
|
8 |
38 |
3 5 6 |
|
9 2 |
39 |
1 2 4 457 7 |
|
5 0 |
40 |
0 1 1 3 6 7 |
|
5 4 2 |
41 |
0 2 5 6 |
|
7 3 3 1 |
42 |
2 |
|
4 0 0 |
43 |
0 |
|
5 5 3 |
44 |
|
|
4 1 |
45 |
|
(2)用茎叶图处理现有的数据不仅可以看出数据的分布状况,而且可以看出每组中的具体数据.
(3)通过观察茎叶图,可以发现品种A的平均每亩产量为411.1千克,品种B的平均亩产量为397.8千克.由此可知,品种A的平均亩产量比品种B的平均亩产量高.但品种A的亩产量不够稳定,而品种B的亩产量比较集中D平均产量附近.
10.(2009安徽卷理)(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区.B肯定是受A感染的.对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是 .同样也假定D受A、B和C感染的概率都是
.同样也假定D受A、B和C感染的概率都是 .在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量.写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
.在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量.写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
本小题主要考查古典概型及其概率计算,考查取有限个值的离散型随机变量及其分布列和均值的概念,通过设置密切贴近现实生活的情境,考查概率思想的应用意识和创新意识。体现数学的科学价值。本小题满分12分。
解:随机变量X的分布列是
|
X |
1 |
2 |
3 |
|
P |
 |
 |
 |
X的均值为
附:X的分布列的一种求法
共有如下6种不同的可能情形,每种情形发生的概率都是 :
:
|
① |
② |
③ |
④ |
⑤ |
⑥ |
|
A-B-C-D |
A-B-C └D |
A-B-C └D |
A-B-D └C |
A-C-D └B |
 |
在情形①和②之下,A直接感染了一个人;在情形③、④、⑤之下,A直接感染了两个人;在情形⑥之下,A直接感染了三个人。
9.(2009全国卷Ⅰ理)(本小题满分12分)(注意:在试题卷上作答无效)
甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束,假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立,已知前2局中,甲、乙各胜1局。
(I)求甲获得这次比赛胜利的概率;
(II)设 表示从第3局开始到比赛结束所进行的局数,求
表示从第3局开始到比赛结束所进行的局数,求 得分布列及数学期望。
得分布列及数学期望。
分析:本题较常规,比08年的概率统计题要容易。
需提醒的是:认真审题是前提,部分考生由于考虑了前两局的概率而导致失分,这是很可惜的,主要原因在于没读懂题。
另外,还要注意表述,这也是考生较薄弱的环节。
8.(2009全国卷Ⅱ文)(本小题满分12分)
某车间甲组有10名工人,其中有4名女工人;乙组有10名工人,其中有6名女工人。现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取4名工人进行技术考核。
(Ⅰ)求从甲、乙两组各抽取的人数;
(Ⅱ)求从甲组抽取的工人中恰有1名女工人的概率;
(Ⅲ)求抽取的4名工人中恰有2名男工人的概率。. 

解析:本题考查概率统计知识,要求有正确理解分层抽样的方法及利用分类原理处理事件概率的能力,第一问直接利用分层统计原理即可得人数,第二问注意要用组合公式得出概率,第三问关键是理解清楚题意以及恰有2名男工人的具体含义,从而正确分类求概率。
解:(I)由于甲、乙两组各有10名工人,根据分层抽样原理,要从甲、乙两组中共抽取4名工人进行技术考核,则从每组各抽取2名工人。
(II)记 表示事件:从甲组抽取的工人中恰有1名女工人,则
表示事件:从甲组抽取的工人中恰有1名女工人,则



(III) 表示事件:从甲组抽取的2名工人中恰有
表示事件:从甲组抽取的2名工人中恰有 名男工人,
名男工人,
 表示事件:从乙组抽取的2名工人中恰有
表示事件:从乙组抽取的2名工人中恰有 名男工人,
名男工人,
 表示事件:抽取的4名工人中恰有2名男工人。.
表示事件:抽取的4名工人中恰有2名男工人。. 

 与
与 独立,
独立, ,且
,且
故 


7.(2009山东卷文)(本小题满分12分)
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
|
|
轿车A |
轿车B |
轿车C |
|
舒适型 |
100 |
150 |
z |
|
标准型 |
300 |
450 |
600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1) 求z的值. 

(2) 用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3) 用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
解: (1).设该厂本月生产轿车为n辆,由题意得, ,所以n=2000. z=2000-100-300-150-450-600=400
,所以n=2000. z=2000-100-300-150-450-600=400
(2) 设所抽样本中有m辆舒适型轿车,因为用分层抽样的方法在C类轿车中抽取一个容量为5的样本,所以 ,解得m=2也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作S1,S2;B1,B2,B3,则从中任取2辆的所有基本事件为(S1, B1), (S1, B2) , (S1,
B3) (S2 ,B1), (S2 ,B2), (S2
,B3),( (S1, S2),(B1 ,B2),
(B2 ,B3) ,(B1 ,B3)共10个,其中至少有1辆舒适型轿车的基本事件有7个基本事件: (S1, B1),
(S1, B2) , (S1, B3) (S2 ,B1),
(S2 ,B2), (S2 ,B3),( (S1,
S2),所以从中任取2辆,至少有1辆舒适型轿车的概率为
,解得m=2也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作S1,S2;B1,B2,B3,则从中任取2辆的所有基本事件为(S1, B1), (S1, B2) , (S1,
B3) (S2 ,B1), (S2 ,B2), (S2
,B3),( (S1, S2),(B1 ,B2),
(B2 ,B3) ,(B1 ,B3)共10个,其中至少有1辆舒适型轿车的基本事件有7个基本事件: (S1, B1),
(S1, B2) , (S1, B3) (S2 ,B1),
(S2 ,B2), (S2 ,B3),( (S1,
S2),所以从中任取2辆,至少有1辆舒适型轿车的概率为 .
.
(3)样本的平均数为 ,
,
那么与样本平均数之差的绝对值不超过0.5的数为9.4, 8.6, 9.2, 8.7, 9.3, 9.0这6个数,总的个数为8,所以该数与样本平均数之差的绝对值不超过0.5的概率为 .
.
[命题立意]:本题为概率与统计的知识内容,涉及到分层抽样以及古典概型求事件的概率问题.要读懂题意,分清类型,列出基本事件,查清个数.,利用公式解答.
6.(2009山东卷理)(本小题满分12分)
在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率q 为0.25,在B处的命中率为q
为0.25,在B处的命中率为q ,该同学选择先在A处投一球,以后都在B处投,用
,该同学选择先在A处投一球,以后都在B处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
 |
0
|
2
|
3 |
4 |
5 |
  p p
|
0.03
|
P1
|
P2 |
P3
|
P4
|
(1) 求q 的值;
的值; 

(2) 求随机变量 的数学期望E
的数学期望E ;
;
(3) 试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
解:(1)设该同学在A处投中为事件A,在B处投中为事件B,则事件A,B相互独立,且P(A)=0.25, ,
P(B)= q
,
P(B)= q ,
, .
.
根据分布列知:  =0时
=0时 =0.03,所以
=0.03,所以 ,q
,q =0.8.
=0.8.
(2)当 =2时, P1=
=2时, P1=


 =0.75 q
=0.75 q (
(
 )×2=1.5 q
)×2=1.5 q (
(
 )=0.24
)=0.24
当 =3时, P2 =
=3时, P2 = =0.01,
=0.01,
当 =4时, P3=
=4时, P3= =0.48,
=0.48,
当 =5时, P4=
=5时, P4=
 =0.24
=0.24
所以随机变量 的分布列为
的分布列为
 |
0
|
2
|
3 |
4 |
5 |
|
p
|
0.03
|
0.24
|
0.01 |
0.48
|
0.24
|
随机变量 的数学期望
的数学期望
(3)该同学选择都在B处投篮得分超过3分的概率为

 ;
;
该同学选择(1)中方式投篮得分超过3分的概率为0.48+0.24=0.72.
由此看来该同学选择都在B处投篮得分超过3分的概率大.
[命题立意]:本题主要考查了互斥事件的概率,相互独立事件的概率和数学期望,以及运用概率知识解决问题的能力.
5.(2009北京卷理)(本小题共13分)
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)求这名学生在上学路上因遇到红灯停留的总时间 的分布列及期望.
的分布列及期望.
[解析]本题主要考查随机事件、互斥事件、相互独立事件等概率知识、考查离散型随机变量的分布列和期望等基础知识,考查运用概率与统计知识解决实际问题的能力.
(Ⅰ)设这名学生在上学路上到第三个路口时首次遇到红灯为事件A,因为事件A等于事件“这名学生在第一和第二个路口没有遇到红灯,在第三个路口遇到红灯”,所以事件A的概率为 .
.
(Ⅱ)由题意,可得 可能取的值为0,2,4,6,8(单位:min).
可能取的值为0,2,4,6,8(单位:min).
事件“ ”等价于事件“该学生在路上遇到
”等价于事件“该学生在路上遇到 次红灯”(
次红灯”( 0,1,2,3,4),
0,1,2,3,4),
∴ ,
,
∴即 的分布列是
的分布列是
 |
0 |
2 |
4 |
6 |
8 |
 |
 |
 |
 |
 |
 |
∴ 的期望是
的期望是 .
.
4.(2009北京卷文)(本小题共13分)
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率.
[解析]本题主要考查随机事件、互斥事件、相互独立事件等概率的基础知识,考查运用概率知识解决实际问题的能力.
(Ⅰ)设这名学生在上学路上到第三个路口时首次遇到红灯为事件A,因为事件A等于事件“这名学生在第一和第二个路口没有遇到红灯,在第三个路口遇到红灯”,所以事件A的概率为 .
.
(Ⅱ)设这名学生在上学路上因遇到红灯停留的总时间至多是4min为事件B,这名学生在上学路上遇到 次红灯的事件
次红灯的事件 .
.
则由题意,得 ,
,
 .
.
由于事件B等价于“这名学生在上学路上至多遇到两次红灯”,
∴事件B的概率为 .
.
3.(2009浙江卷理)(本题满分14分)在 这
这 个自然数中,任取
个自然数中,任取 个数.
个数.
(I)求这 个数中恰有
个数中恰有 个是偶数的概率;
个是偶数的概率;
(II)设 为这
为这 个数中两数相邻的组数(例如:若取出的数为
个数中两数相邻的组数(例如:若取出的数为 ,则有两组相邻的数
,则有两组相邻的数
 和
和 ,此时
,此时 的值是
的值是 ).求随机变量
).求随机变量 的分布列及其数学期望
的分布列及其数学期望 .
.
解析:(I)记“这3个数恰有一个是偶数”为事件A,则 ;.
;. 

(II)随机变量 的取值为
的取值为 的分布列为
的分布列为
 |
0 |
1 |
2 |
|
P |
 |
 |
 |
所以 的数学期望为
的数学期望为 .
. 

2.(2009广东卷理)(本小题满分12分)
根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
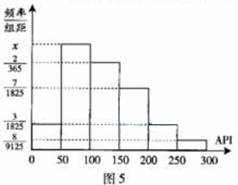
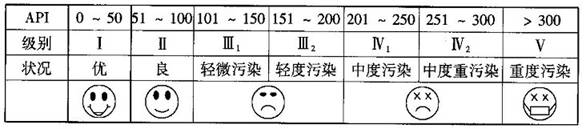 对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间 ,
, ,
, ,
, ,
, ,
, 进行分组,得到频率分布直方图如图5.
进行分组,得到频率分布直方图如图5.
(1)求直方图中 的值;
的值;
(2)计算一年中空气质量分别为良和轻微污染的天数;
(3)求该城市某一周至少有2天的空气质量为良或轻微污染的概率.
(结果用分数表示.已知 ,
, ,
,

 ,
, )
)
解:(1)由图可知


 ,解得
,解得 ;
;
(2) ;
;
(3)该城市一年中每天空气质量为良或轻微污染的概率为 ,则空气质量不为良且不为轻微污染的概率为
,则空气质量不为良且不为轻微污染的概率为 ,一周至少有两天空气质量为良或轻微污染的概率为
,一周至少有两天空气质量为良或轻微污染的概率为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com