
30.(2009重庆卷理)(本小题满分13分,(Ⅰ)问7分,(Ⅱ)问6分)
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为 和
和 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(Ⅰ)两种大树各成活1株的概率;
(Ⅱ)成活的株数 的分布列与期望.
的分布列与期望.


解:设 表示甲种大树成活k株,k=0,1,2
表示甲种大树成活k株,k=0,1,2
 表示乙种大树成活l株,l=0,1,2
表示乙种大树成活l株,l=0,1,2
则 ,
, 独立. 由独立重复试验中事件发生的概率公式有
独立. 由独立重复试验中事件发生的概率公式有
 ,
,  .
.
据此算得
 ,
,  ,
,  .
.
.
. 

 ,
,
 ,
,  .
.
(Ⅰ) 所求概率为
 .
.
(Ⅱ) 解法一:
 的所有可能值为0,1,2,3,4,且.
的所有可能值为0,1,2,3,4,且. 

 ,
,
 ,
,

= ,
,
 .
.
 .
.
综上知 有分布列
有分布列
 |
0 |
1 |
2 |
3 |
4 |
|
P |
1/36 |
1/6 |
13/36 |
1/3 |
1/9 |
从而, 的期望为
的期望为

 (株)
(株)
解法二:
分布列的求法同上
令 分别表示甲乙两种树成活的株数,则
分别表示甲乙两种树成活的株数,则


故有 .
. 

从而知
29.(2009福建卷文)(本小题满分12分)
袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球
(I)试问:一共有多少种不同的结果?请列出所有可能的结果;


(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
解:(I)一共有8种不同的结果,列举如下:
(红、红、红、)、(红、红、黑)、(红、黑、红)、(红、黑、黑)、(黑、红、红)、(黑、红、黑)、(黑、黑、红)、(黑、黑、黑)
(Ⅱ)记“3次摸球所得总分为5”为事件A
事件A包含的基本事件为:(红、红、黑)、(红、黑、红)、(黑、红、红)事件A包含的基本事件数为3
由(I)可知,基本事件总数为8,所以事件A的概率为 .
. 

28.(2009四川卷理)(本小题满分12分)
为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡)。某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游,其中 是省外游客,其余是省内游客。在省外游客中有
是省外游客,其余是省内游客。在省外游客中有 持金卡,在省内游客中有
持金卡,在省内游客中有 持银卡。.
持银卡。. 

(I)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率;
(II)在该团的省内游客中随机采访3名游客,设其中持银卡人数为随机变量 ,求
,求 的分布列及数学期望
的分布列及数学期望 。
。
本小题主要考察相互独立事件、互斥事件、随机变量的分布列、数学期望等概率计算,考察运用概率只是解决实际问题的能力。
解:(Ⅰ)由题意得,省外游客有27人,其中9人持金卡;省内游客有9人,其中6人持银卡。设事件 为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
事件 为“采访该团3人中,1人持金卡,0人持银卡”,
为“采访该团3人中,1人持金卡,0人持银卡”,
事件 为“采访该团3人中,1人持金卡,1人持银卡”。
为“采访该团3人中,1人持金卡,1人持银卡”。 
 .
. 




所以在该团中随机采访3人,恰有1人持金卡且持银卡者少于2人的概率是 。
。
…………………………………………………………6分
(Ⅱ) 的可能取值为0,1,2,3
的可能取值为0,1,2,3
 ,
,  .
. 

 ,
, ,.
,.


所以 的分布列为
的分布列为
 |
0 |
1 |
2 |
3 |
 |
 |
 |
 |
 |
所以 , ……………………12分
, ……………………12分
27.(2009湖南卷理)(本小题满分12分).

为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的. 、
、 、
、 ,现在3名工人独立地从中任选一个项目参与建设。
,现在3名工人独立地从中任选一个项目参与建设。


(I)求他们选择的项目所属类别互不相同的概率;
(II)记 为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数,求
为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数,求 的分布列及数学期望。
的分布列及数学期望。
解:记第1名工人选择的项目属于基础设施工程、民生工程和产业建设工程分别为事件  ,
, ,
, ,i=1,2,3.由题意知
,i=1,2,3.由题意知
 相互独立,
相互独立,
 相互独立,
相互独立,
 相互独立,
相互独立, ,
, ,
, (i,j,k=1,2,3,且i,j,k互不相同)相互独立,且P(
(i,j,k=1,2,3,且i,j,k互不相同)相互独立,且P( )=,P(
)=,P( )=
)= ,P(
,P( )=
)=
(1) 他们选择的项目所属类别互不相同的概率
P=3!P(

 )=6P(
)=6P( )P(
)P( )P(
)P( )=6
)=6




 =
=
(2) 解法1 设3名工人中选择的项目属于民生工程的人数为 ,由己已知,
,由己已知, -B(3,
-B(3, ),且
),且 =3
=3 。
。
所以P( =0)=P(
=0)=P( =3)=
=3)=
 =
= ,.
,.

P( =1)=P(
=1)=P( =2)=
=2)= 

 =
=



P( =2)=P(
=2)=P( =1)=
=1)=

 =
=
P( =3)=P(
=3)=P( =0)=
=0)= 
 =
=

故 的分布是
的分布是
 |
0 |
1 |
2 |
3 |
|
P |
 |
 |
 |
 |
 的数学期望E
的数学期望E =0
=0
 +1
+1
 +2
+2
 +3
+3
 =2
=2
解法2 第i名工人选择的项目属于基础工程或产业工程分别为事件 ,
,
i=1,2,3 ,由此已知, ·D,
·D, 相互独立,且
相互独立,且
P( )-(
)-( ,
, )= P(
)= P( )+P(
)+P( )=
)= +
+ =
= .
. 
所以 --
-- ,既
,既 ,
,


故 的分布列是
的分布列是
 |
 |
1 |
2 |
3 |
 |
 |
 |
 |
 |
所以
由事件的独立性的

解答2(Ⅰ)设事件A表示“一个月内被投诉2次”设事件B表示“一个月内被投诉的次数不超过1次”
所以
(Ⅱ)同解答1(Ⅱ)
26.(2009宁夏海南卷文)(本小题满分12分)
某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(Ⅰ)A类工人中和B类工人各抽查多少工人?. 

(Ⅱ)从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
|
生产能力分组 |
 |
 |
 |
 |
 |
|
人数 |
4 |
8 |
 |
5 |
3 |
表2:
|
生产能力分组 |
 |
 |
 |
 |
|
人数 |
6 |
y |
36 |
18 |
(1) 先确定 ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
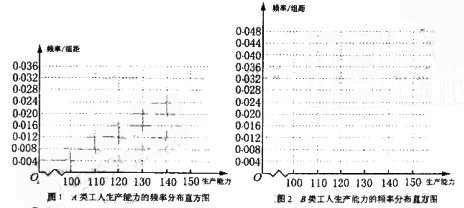
(ii)分别估计 类工人和
类工人和 类工人生产能力的平均数,并估计该工厂工人和生产能力的平均数(同一组中的数据用该区间的中点值作代表)。
类工人生产能力的平均数,并估计该工厂工人和生产能力的平均数(同一组中的数据用该区间的中点值作代表)。
(19)解:
(Ⅰ) 类工人中和
类工人中和 类工人中分别抽查25名和75名。
......4分
类工人中分别抽查25名和75名。
......4分
(Ⅱ)(ⅰ)由 ,得
,得 ,
,
 ,得
,得 。
。


频率分布直方图如下
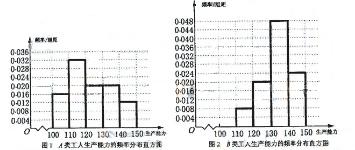 ......8分
......8分
从直方图可以判断: 类工人中个体间的差异程度更小。
......9分
类工人中个体间的差异程度更小。
......9分
(ii)  ,
,
 ,
,



A类工人生产能力的平均数,B类工人生产能力的平均数以及全厂工人生产能力的平均数的估计值分别为123,133.8和131.1.
25.(2009陕西卷文)(本小题满分12分)
椐统计,某食品企业一个月内被消费者投诉的次数为0,1,2的概率分别为0.4,0.5,0.1
(Ⅰ) 求该企业在一个月内共被消费者投诉不超过1次的概率;
(Ⅱ)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率。
解析:解答1(Ⅰ)设事件A表示“一个月内被投诉的次数为0”事件B表示“一个月内被投诉的次数为1”
所以
(Ⅱ)设事件 表示“第
表示“第 个月被投诉的次数为0”事件
个月被投诉的次数为0”事件 表示“第
表示“第 个月被投诉的次数为1”事件
个月被投诉的次数为1”事件 表示“第
表示“第 个月被投诉的次数为2”事件D表示“两个月内被投诉2次”
个月被投诉的次数为2”事件D表示“两个月内被投诉2次”
所以
所以两个月中,一个月被投诉2次,另一个月被投诉0次的概率为
24.(本小题满分12分) 某食品企业一个月内被消费者投诉的次数用 表示,.
表示,. 
椐统计,随机变量 的概率分布如下:
的概率分布如下:
 |
0 |
1 |
2 |
3 |
|
p |
0.1 |
0.3 |
2a |
a |
(Ⅰ)求a的值和 的数学期望;
的数学期望;
(Ⅱ)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率。
解析:(Ⅰ)由概率分布的性质知,  则
则 的分布列为
的分布列为
 |
0 |
1 |
2 |
3 |
|
p |
0.1 |
0.3 |
0.4 |
0.2 |

(Ⅱ)设事件 表示”2个月内共被投诉2次" 事件
表示”2个月内共被投诉2次" 事件 表示”2个月内有一个月被投诉2次,另一个月被投诉0次" ,事件
表示”2个月内有一个月被投诉2次,另一个月被投诉0次" ,事件 表示”2个月内每个月均被投诉1次" 则由事件的独立性可得
表示”2个月内每个月均被投诉1次" 则由事件的独立性可得


 故该企业在这两个月共被投诉2次的概率为0.17.
.
故该企业在这两个月共被投诉2次的概率为0.17.
. 

23.(2009四川卷文)(本小题满分12分)
为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡)。某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游,其中 是省外游客,其余是省内游客。在省外游客中有
是省外游客,其余是省内游客。在省外游客中有 持金卡,在省内游客中有
持金卡,在省内游客中有 持银卡。
持银卡。 
 .
. 
(I)在该团中随机采访2名游客,求恰有1人持银卡的概率;
(II)在该团中随机采访2名游客,求其中持金卡与持银卡人数相等的概率.
[解析]I)由题意得,省外游客有27人,其中9人持金卡;省内游客有9人,其中6人持银卡.
设事件A为“采访该团2人,恰有1人持银卡”,则

所以采访该团2人,恰有1人持银卡的概率是 . …………………………………6分
. …………………………………6分
(II)设事件B为“采访该团2人,持金卡人数与持银卡人数相等”,可以分为:
事件B1为“采访该团2人,持金卡0人,持银卡0人”,或事件B2为“采访该团2人,持金卡1人,持银卡1人”两种情况,则

所以采访该团2人,持金卡与持银卡人数相等的概率是 . ……………………12分
. ……………………12分
22.(2009全国卷Ⅰ文)(本小题满分12分)(注意:在试题卷上作答无效)
甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束。假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立。已知前2局中,甲、乙各胜1局。
(Ⅰ)求再赛2局结束这次比赛的概率;
(Ⅱ)求甲获得这次比赛胜利的概率。
[解析]本小题考查互斥事件有一个发生的概率、相互独立事件同时发生的概率,综合题。
解:记“第 局甲获胜”为事件
局甲获胜”为事件 ,“第
,“第 局甲获胜”为事件
局甲获胜”为事件 。
。
(Ⅰ)设“再赛2局结束这次比赛”为事件A,则
 ,由于各局比赛结果相互独立,故
,由于各局比赛结果相互独立,故

 。
。
(Ⅱ)记“甲获得这次比赛胜利”为事件B,因前两局中,甲、乙各胜1局,故甲获得这次比赛胜利当且仅当在后面的比赛中,甲先胜2局,从而
 ,由于各局比赛结果相互独立,故
,由于各局比赛结果相互独立,故

 .
. 

21.(本小题满分12分)
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表:
甲厂
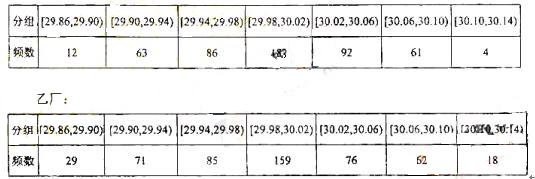
(1) 试分别估计两个分厂生产的零件的优质品率;
(2) 由于以上统计数据填下面 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
|
|
甲 厂 |
乙 厂 |
合计 |
|
优质品 |
|
|
|
|
非优质品 |
|
|
|
|
合计 |
|
|
|
附:


解:(Ⅰ)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为 ; ……6分
; ……6分
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为
(Ⅱ)
|
|
甲厂 |
乙厂 |
合计 |
|
优质品 |
360 |
320 |
680 |
|
非优质品 |
140 |
180 |
320 |
|
合计 |
500 |
500 |
1000 |
……8分



所以有99%的把握认为“两个分厂生产的零件的质量有差异”。 ……12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com