
21.解:(1)由条件得M(0,-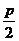 ),F(0,
),F(0,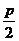 ).设直线AB的方程为
).设直线AB的方程为
y=kx+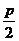 ,A(
,A(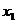 ,
,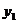 ),B(
),B(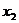 ,
,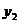 ).
).
则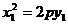 ,
,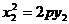 ,Q(
,Q(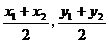 ).
).
由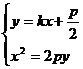 得
得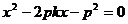 .
.
∴由韦达定理得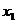 +
+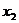 =2pk,
=2pk,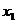 ·
·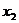 =-
=-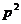
从而有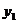
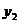 =
=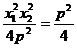
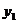 +
+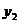 =k(
=k(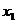 +
+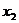 )+p=
)+p=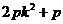 ………………(4分)
………………(4分)
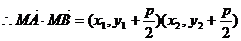
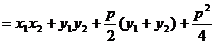

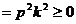
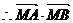 的取值范围是
的取值范围是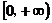 .……………………………………………(6分)
.……………………………………………(6分)
(2)抛物线方程可化为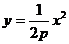 ,求导得
,求导得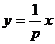 .
.
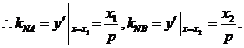
∴切线NA的方程为:y- 即
即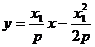 .
.
切线NB的方程为: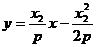 ………………………………………(8分)
………………………………………(8分)
由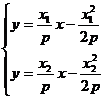 解得
解得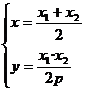 ∴N(
∴N(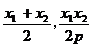 )
)
从而可知N点Q点的横坐标相同但纵坐标不同.
∴NQ∥OF.即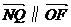 …………………………………………………………(9分)
…………………………………………………………(9分)
又由(Ⅰ)知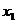 +
+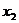 =2pk,
=2pk,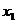 ·
·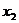 =-p
=-p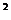 ∴N(pk,-
∴N(pk,-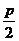 ).……………(11分)
).……………(11分)
而M(0,-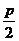 ) ∴
) ∴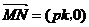
又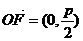 . ∴
. ∴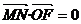 .………………………………………………(12分)
.………………………………………………(12分)
20.解:由题意得: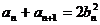 ①…………………………………1分
①…………………………………1分
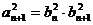 ②…………………………………2分
②…………………………………2分
∵{an}、{bn}都是各项均为正的数列
由②得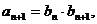
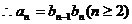 代入①得…………………………………4分
代入①得…………………………………4分
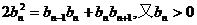
∴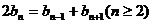 …………………………………7分
…………………………………7分
∴数列{bn}是等差数列…………………………………8分
由a1=1,b1=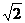 及①②两式得
及①②两式得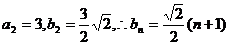 ……………12分
……………12分
19.解: (1)D为A1C1的中点. …………………………………2分
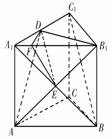 连结A1B与AB1交于E,
连结A1B与AB1交于E,
则E为A1B的中点,DE为平面AB1D与平面A1BC1的交线,
∵BC1∥平面AB1D
∴BC1∥DE,∴D为A1C1的中点. ……………………………6分
(2) 解法一:过D作DF⊥A1B1于F,
由正三棱柱的性质,AA1⊥DF,∴DF⊥平面AB1,
连结EF、DE,在正三角形A1B1C1中,
∵D是A1C1的中点,∴B1D=A1B1=a,…………………7分
又在直角三角形AA1D中,
∵AD==a,∴AD=B1D. …………………………………8分
∴DE⊥AB1,∴可得EF⊥AB1,
则∠DEF为二面角A1-AB1-D的平面角. …………………………………10分
可求得DF=a,
∵△B1FE∽△B1AA1,
得EF=a,∴∠DEF=,即为所求. ……………12分
(2)解法(二)(空间向量法)
建立如图所示空间直角坐标系,则
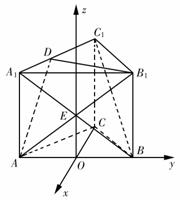 A(0,-a,0)、B1(0,a,a)、C1(-a,0,a)、
A(0,-a,0)、B1(0,a,a)、C1(-a,0,a)、
A1(0,-a,a)、D(-a,-a,a).
∴=(0,a,a),=(-a,-a,0). ……8分
设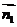 =(x,y,z)是平面AB1D的一个法向量,
=(x,y,z)是平面AB1D的一个法向量,
则可得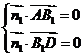 ,即
,即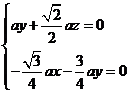 .
.
∴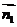 =(-,1,-). …………………………10分
=(-,1,-). …………………………10分
又平面AB1的一个法向量
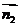 ==(-a,0,0),设n1与n2的夹角是θ,
==(-a,0,0),设n1与n2的夹角是θ,
则 cosθ=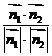 =.
=.
又可知二面角A1-AB1-D是锐角,
∴二面角A1-AB1-D的大小是.
18.解:(1)配量合理的概率为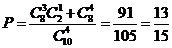 ………………………6分
………………………6分
(2)两次检查看成两次独立实验∴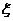 -B(
-B(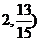
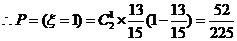 ……………………………………11分
……………………………………11分
答:两次检查得到结果不一致的概率为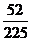 ………………………………………………12分
………………………………………………12分
17.解:(1)依题意按向量m平移g(x)得
f(x)-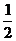 =
=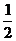 sin[2(x+
sin[2(x+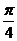 )+
)+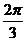 ]……………………………………(2分)
]……………………………………(2分)
得f(x)=-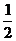 sin(2x+
sin(2x+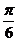 )+
)+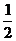 ……………………………………………(4分)
……………………………………………(4分)
又f(x)=acos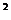 (x+
(x+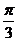 )+b=-
)+b=-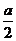 sin(2x+
sin(2x+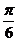 )+
)+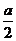 +b
+b
比较得a=1,b=0…………………………………………………………………(6分)
(2)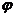 (x)=g(x)-
(x)=g(x)-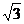 f(x)=
f(x)=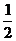 sin(2x+
sin(2x+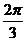 )-
)-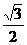 cos(2x+
cos(2x+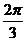 )-
)-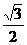
=sin(2x+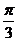 )-
)-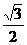 ………………………………………………………(9分)
………………………………………………………(9分)
2kπ-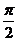 ≤2x+
≤2x+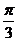 ≤2kπ+
≤2kπ+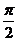 (k∈Z)
(k∈Z)
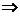 kπ-
kπ-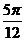 ≤x≤kπ+
≤x≤kπ+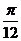 (k∈Z)
(k∈Z)
∴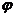 (x)的单调增区间为[kπ-
(x)的单调增区间为[kπ-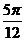 ,kπ+
,kπ+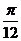 ](k∈Z)………………(12分)
](k∈Z)………………(12分)
|
13.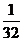 14.60 15.
14.60 15.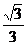 16. ①③④
16. ①③④
22.(本小题满分14分)已知函数f(x)=x3-ax2,其中a为实常数.
(1)设当x∈(0,1)时,函数y = f(x)图象上任一点P处的切线的斜线率为k,若k≥-1,求a的取值范围;
(2)当x∈[-1,1]时,求函数y=f(x)+a(x2-3x)的最大值.
2007-2008学年度南昌市高三第一轮复习训练题
数学(二十) (文科 综合卷二) 参考答案
综合卷二) 参考答案
21.(本小题满分13分)直线AB过抛物线x2=2py(p>0)的焦点F,并与其相交于A、B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,O是坐标原点.
(1)求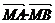 的取值范围;
的取值范围;
(2)过A、B两点分别作此抛物线的切线,两切线相交于N点.。求证: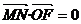 ,
,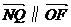 .
.
20.(本小题满分12分)已知数列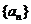 、
、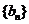 都是各项均为正的数列,
都是各项均为正的数列,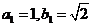 ,对任意的自然数n都有
,对任意的自然数n都有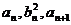 成等差数列,
成等差数列, 成等比数列.
成等比数列.
(1)试问数列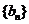 是否是等差数列?并求
是否是等差数列?并求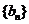 的通项公式.
的通项公式.
19.(本小题满分12分)如图正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为a,若经过对角线AB1且与对角线BC1平行的平面交上底面于DB1.
(1)试确定点D的位置,并证明你的结论;
(2)求二面角A1-AB1-D的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com