
82.答案:y=-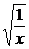 (x>0)
(x>0)
解析:由y=x-2(x<0 解出x2=
解出x2=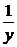 (x<0
(x<0 ,x=-
,x=-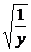 (y>0),将x与y对换,得y=-
(y>0),将x与y对换,得y=-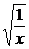 (x>0).
(x>0).
81.答案:x=1
解析:将方程变形得log2(32x-5)=log24(3x-2),
|
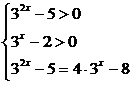
由③得32x-4·3x+3=0,即(3x-3)(3x-1)=0,
解得:x=1或x=0.
将x=1与x=0分别代入①、②中检验,知x=1是原方程的根,x=0是增根.
80.答案:{x|1<x<2}
解析:x应满足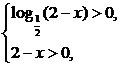
即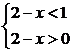 解得1<x<2.
解得1<x<2.
故函数的定义域为{x|1<x<2}.
79.答案:x=-5
解析:原方程变为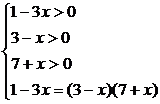
所以有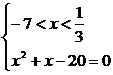 所以x=-5.
所以x=-5.
77.答案: 或
或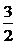
解析:因指数函数y=ax为单调函数,所以有|a2-a|=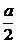 ,解得a=
,解得a= 或a=
或a=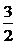 .
.
※78.答案:8
解析:我们用逐一验证法.
(1)1→2→5→7→8;10天
(2)1→3→4→6→7→8;10天
(3)1→3→4→5→6→7→8;9天
(4)1→3→4→5→7→8;8天
(5)1→2→5→6→7→8;11天
评述:主要考查用数学思想解决实际问题的能力.
76.答案:4
解析:当x≤0时,y的最大值为3;当0<x≤1时,y的最大值为4;当x>1时,y的最大值不存在,但此时y<4.故y的最大值是4.
75.答案:(x-2)3+1
解析:由y=(x-1) +2得(x-1)
+2得(x-1) =y-2,x-1=(y-2)3,x=(y-2)3+1,所以所求的函数的反函数为y=(x-2)3+1.
=y-2,x-1=(y-2)3,x=(y-2)3+1,所以所求的函数的反函数为y=(x-2)3+1.
74.答案:2
解析:lg20+log10025=lg20+ lg25=1+lg2+lg5=1+lg10=2.
lg25=1+lg2+lg5=1+lg10=2.
73.答案:[9,+∞
解析一:由ab=a+b+3≥2 +3(等号成立条件为a=b),整理得ab-2
+3(等号成立条件为a=b),整理得ab-2 -3≥0,(
-3≥0,( -3)(
-3)( +1)≥0,∴
+1)≥0,∴ ≥3,∴ab≥9.
≥3,∴ab≥9.
解析二:由ab=a+b+3,可得:b=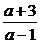 (a>0,b>0),∴a>1,又ab=a·
(a>0,b>0),∴a>1,又ab=a·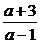 =[(a-1)+1]
=[(a-1)+1]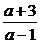 =(a+3)+
=(a+3)+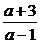 =a-1+4+
=a-1+4+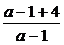 =(a-1)+
=(a-1)+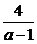 +5≥2
+5≥2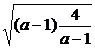 +5=9.等号成立条件为a-1=
+5=9.等号成立条件为a-1=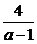 ,即a=3.
,即a=3.
评述:本题考查不等式和函数的基本性质以及推理论证能力.
71.答案:[3,+∞)
解析:因为函数f(x)=log2x+1(x≥4)的值域是[3,+∞),∴反函数f-1(x)的定义域是[3,+∞).
评述:本题考查了反函数的一个性质:原函数的值域是反函数的定义域.
※72.答案:4
解析:设工序c所需工时数为x天,由题设关键路线是a→c→e→g.需工时1+x+4+1=10.∴x=4,即工序c所需工时数为4天.
评述:本题新颖,属于“优选法”题型.主要考查工序流程图内容的基础知识及数形结合对图形分析的能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com