58.答案：f^－1(0)=a且f^－1(x)＜x，x∈A或y=f^－1(x)的图象在直线y=x的下方，且与y轴的交点为(0，a)

解析：因为y=f(x)有反函数，则y=f(x)与其反函数y=f^－1(x)关于y=x对称.

由方程f(x)=0有解x=a，则f(a)=0，又f(x)＞x，说明在定义域D内，函数y=

f(x)的图象在直线y=x的上方，而y=f(x)的反函数y=f^－1(x)与y=f(x)的图象关于直线y=x对称.因此，从代数角度回答有f^－1(0)=a且f^－1(x)＜x.从几何角度回答有y=f^－1(x)的图象在直线y=x的下方，且与y轴的交点为(0，a).

^※59.答案：1995，2000(或1985，1990)

解析：从图中的数据可观察到：从1995年到2000年的五年间居住面积增长最快.应填1995，2000.

如果从增长的速度思考，应填1985，1990.

评述：这是小学六年级学习的条形统计图，放在高考题中，充分反映了高考的命题思想，独具匠心，妙哉！本题考查了考生读图识图能力以及用数学方法解决问题的能力.由于题设中没有对增长量或增长速度做明确要求.两种结果都对(只填一个即可).

57.答案：－1

解析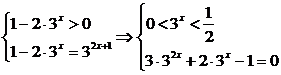：得3^x=t

∴

∴t=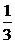

∴3^x=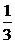，∴x=－1

56.答案：②④

解析：y=(－x)f［(－x)²］=－xf(x²)=－y

y=f(－x)－f(x)=－y

55.答案：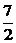

解析：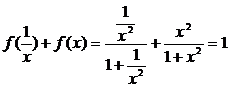

∴f(1)+［f(2)+f()］+［f(3)+f(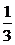)］+［f(4)+f()］=+1+1+1=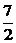

评述：在f(2)+f()=1的基础上判断f(x)+f(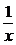)=1， 问题便迎刃而解.

54.答案：(0，0)，(1，1)

解法一：由反函数的意义和性质可知，如果原函数为增函数，则其图象与反函数图象关于直线y=x对称，两图象的交点必在y=x直线上，因此题目所求可转化为求y=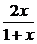(x∈(－1，+∞))图象与y=x直线的交点.

解法二：求出反函数y=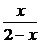，解其与原函数y=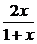的交点.

评述：在解法一中，函数的图象若与其反函数的图象相交，交点不一定都在直线y=x上，这一点有许多同学弄不清楚，只有原函数为单调增函数，上述结论才成立.

53.答案：－1

解析：因为x≥0时，f(x)=log₃(1+x)，又f(x)为奇函数，所以f(－x)=－f(x)，设x＜0，所以f(x)=－f(－x)=－f(1－x)，所以f(－2)=－log₃3=－1.

52.答案：－3＜x＜2

解析：由题意得3－2x－x²＞0，可得－3＜x＜2

51.答案：6

解析一：因为二次函数y=x²+(a+2)x+3的对称轴为x=1，因此有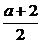－=1.即a=－4，而函数f(x)是定义在［a，b］上的.即a，b关于x=1也对称，所以有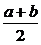=1.解得b=6.

解析二：因为二次函数y=x²+(a+2)x+3的对称轴为x=1.因此，f(x)可表示为f(x)=(x－1)²+c，与原函数表达形式对比可得a+2=－2，∴a=－4.再结合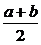=1，解得b=6.

解析三：因为二次函数的对称轴为x=1，因此有：f(x)=f(2－x).将2－x代入y=x²+(a+2)x+3即可求出a=－4，b值同上.

评述：区间［a，b］关于x=1对称是一个必要条件，否则f(x)=f(2－x)将无意义.此题较好地考查了逻辑思维能力.

50.答案：

注：填的正整数倍中的任何一个都正确.

解析：令px－=u，则px=u+，依题意，有：f(u+)=f(u).此式对任意u都成立，而>0且为常数.因此，说明f(x)是一个周期函数，为最小正周期.

评述：利用换元法，紧扣周期函数定义.本题立意：重在知识和技能的灵活运用.

49.答案：C

解法一：注意观察四个选项中的每两个函数，容易发现C中g(x)＝为奇函数，且h(－x)=lg(10^-x+1)+＝lg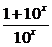+＝lg(10^x+1)－＝h(x)为偶函数，又

g(x)+h(x)=lg(10^x+1)＝f(x)，故应选C.

解法二：由已知有f(x)=g(x)+h(x)，则f(－x)=g(－x)+h(－x)=－g(x)+

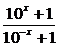h(x)，所以g(x)=［f(x)－f(－x)］＝lg＝lg10^x＝，应选C.

评述：本题考查了奇偶函数、对数函数的概念和性质，要求有较强的运算能力.本题背景新颖，对分析问题和解决问题的能力有较高要求.