28.答案：A

解析：由已知点(a，b)在函数y＝f(x)图象上，又由反函数与原函数的性质知，(b，a)在其反函数y＝g(x)图象上，即g(b)＝a，故选A.

评述：本题主要考查反函数的性质的运用，解法上还可取特殊函数、特殊点加以验证解决.

27.答案：A

解析：由映射的定义及给定法则知，对A中元素取绝对值立即得结论，故选A.

评述：本题主要考查映射的概念，属容易题.

26.答案：C

解析：∵20＝2ⁿ+n，分别将选择支代入检验，知当n＝4时成立.

25.答案：A

解析：∵y＝3^x＞0(x∈R)　 ∴S＝{y|y＞0}；

∵y＝x²－1≥－1(x∈R)

∴T＝{y|y≥－1}　 ∴ST，从而S∩T＝S.

24.答案：A

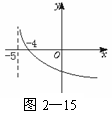
解析：g(x)＝a^x的图象经过一、二象限，f(x)＝a^x+b是将g(x)＝a^x的图象向下平移|b|(b＜－1)个单位而得，因而图象不经过第一象限.

23.答案：A

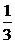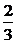解法一：分别将x＝0，x＝1，x＝2代入f(x)＝ax³+bx²+cx+d中，求得d＝0，a＝－b，c＝－b，

∴f(x)＝．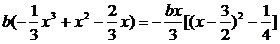

当x∈(－∞,0)时，f(x)＜0，又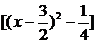＞0，∴b＜0．

x∈(0，1)时，f(x)＞0，又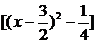＞0，

∴b＜0．

x∈(1,2)时，f(x)＜0，又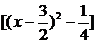＜0，∴b＜0．

x∈(2?+∞)时，f(x)＞0，又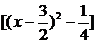＞0，∴b＜0．

故b∈(－∞?0).

解法二：由此题的函数图象可以联想到解高次不等式时所用的图象法

∴a＞0，x₁，x₂，x₃为图象与x轴的交点x₁＝2，x₂＝1，x₃＝0，

∴ax³+bx²+cx+d=a(x－x₁)(x－x₂)(x－x₃)＝a(x－2)(x－1)(x－0)

∴f(x)=ax³－3ax²+2ax，又∵a＞0，∴b＝－3a，b＜0

∴选A

解法三：函数f(x)的图象过原点，即f(0)=0得d=0

又因f(x)的图象过点(1，0)，得f(1)=a+b+c=0　　　　　 ①

由图象得f(－1)＜0，即－a+b－c＜0　　　　　　　　　　　　　　　　 ②

①+②得2b＜0，∴b＜0．

22.答案：B

解析：∵f(－x)＝lg|－x|＝lg|x|＝f(x)是偶函数，又当x∈(0，+∞)时是单调递增，∴当x∈(－∞,0)时，y＝lg|x|单调递减.

20.答案：C

解析：在共同定义域上任取x₁＜x₂，当f(x)是单调递增，则f(x₁)－f(x₂)＜0，

g(x)是单调递减，g(x₁)－g(x₂)＞0，

∴F(x)＝f(x)－g(x)

F(x₁)－F(x₂)=f(x₁)－f(x₂)+g(x₂)－g(x₁)＜0

∴在共同定义域上是单调递增，同理可得

当f(x)是单调递减，g(x)是单调递增时，F(x)=f(x)－g(x)是单调递减．

∴②③正确

^※21.答案：D

解析：因为连线标注的数字表示该段网线单位时间内可通过的最大信息量，∴BC最大是3，BE最大为4，FG最大为6，BH最大为6．

而传递的路途只有4条．

BC-CD-DA，BE-ED-DA，BF-FG-GA，BH-HG-GA

而每条路径允许通过的最大信息量应是一条途径中3段中的最小值，如BC-CD-DA中BC能通过的最大信息量为3，

∴BC-CD-DA段能通过的最大信息量也只能是3．

以此类推能传到的最大信息量为3+4+6+6＝19．

评述：研究此题不需要任何数学知识，考查考生用数学思维解决问题的能力，这是今后高考的命题方向.

19.答案：A

解析：找到原函数的定义域和值域，x∈［0，+∞)，y∈(1，2)

又∵原函数的值域是反函数的定义域，

∴反函数的定义域x∈(1，2)，∴C、D不对．

而1＜x＜2，∴0＜x－1＜1，＞1．

又log₂＞0，即y＞0

∴A正确．

18.答案：A

解析：∵－1＜x＜0，∴0＜x+1＜1，

又∵f(x)＞0，∴0＜2a＜1，∴0＜a＜(可结合函数图象观察)．