17.答案：C

解析：f(x)·f(y)=a^x·a^y=a^x+y=f(x+y).故选C.

评述：本题考查指数的基本运算法则及考生灵敏的思维能力.

16.答案：D

解法一：8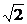＝()⁶，∴f(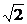⁶)＝log₂＝

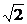解法二：f(x⁶)＝log₂x，∴f(x)＝log₂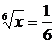log₂x

∴f(8)=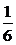log₂8＝．

解法三：∵f(8)=f(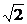⁶)=log₂=.

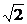15.答案：C

解析：由∵x≤1，∴－x≥－1，1－x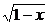≥0，∴≥0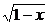，－≤0，∴y≥0．

原函数的值域应与反函数的定义域相同，

∴答案中只有C的定义域满足小于等于0

∴选C

12.答案：A

解析：利用特殊值法，因为λ∈［0，1］，令λ=，则不等式变为：

f()≤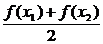，同11题结果.

评述：通过抽象函数知识，考查了学生的抽象思维能力.这是高考命题的方向.

^※13.答案：C

解析:首先要明白“到十·五”末为4年，其次要理解每年比上年增长7.3%的含义,从而得出解析式“十·五”末我国国内年生产总值约为95933×(1+7.3%)⁴.怎样处理(1+7.3%)⁴，显然，不能使其约等于1，在此应用二项式定理(1+7.3%)⁴=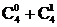·7.3%+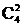·7.3%²+…做近似计算.

^※14.答案：C

解析：该题考查对图表的识别和理解能力，经比较可发现，2月份用电量最多，而2月份气温明显不是最高.因此A项错误.同理可判断出B项错误.由5、6、7三个月的气温和用电量可得出C项正确.

11.答案：A

解析：f()为自变量x₁、x₂中点，对应的函数值即“中点的纵坐标”，［f(x₁)+f(x₂)］为x₁、x₂对应的函数值所对应的点的中点，即“纵坐标的中点”，再结合f(x)函数图象的凹凸性，可得到答案A，这是函数凹凸性的基本应用.

10.答案：B

解析一：该题考查对f(x)=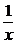图象以及对坐标平移公式的理解，将函数y=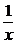的图形变形到y=，即向右平移一个单位，再变形到y=－即将前面图形沿x轴翻转，再变形到y=－+1，从而得到答案B.

解析二：可利用特殊值法，取x=0，此时y=1，取x=2，此时y=0.因此选B.

9.答案：A

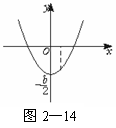
解析：作出函数y=x²+bx+c的大致图象如图2-14.

对称轴为x=－

∵该函数在［0，+∞］上是单调函数.

(由图可知［0，+∞］上是增函数)，只要对称轴横坐标位置在区间［0，+∞的左边，即－≤0，解得b≥0.

8.答案：D

解法一：∵0＜a＜1，x，y＜a，∴log_ax＞log_aa=1，同理log_ay＞1

∴log_ax+log_ay＞2，

即log_axy＞2

解法二：可代入特殊值如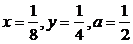，即可解得D答案.

7.答案：B

解析一：①当a＞1时，y=a^x为单调递增函数，在［0，1］上的最值分别为y_max=a¹，

y_min=a⁰=1，∴a+1=3即a=2.

②当0＜a＜1时，y=a^x为单调递减函数，y_max=a⁰=1，y_min=a¹=a，a+1=3，∴a=2与0＜a＜1矛盾，不可能.

解析二：因为y=a^x是单调函数.因此必在区间［0，1］的端点处取得最大值和最小值.因此有a⁰+a¹=3，解得a=2.

评述：因为y=a^x的增减性与a的取值范围有关，所以要将a分情况讨论.该题体现了分类讨论的思想，同时更深层次地研究函数的最值问题.

6.答案：B

解法一：y=log_ax的反函数为y=a^x，而y=log_a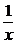的反函数为y=a^－x，因此，它们关于y轴对称.

解法二：因为两个原函数的图象关于x轴对称，而互为反函数的图象关于直线y=x 对称，因此y=log_ax的反函数和y=log_a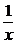的反函数的图象关于y轴对称.

评述：本题考查了两个函数图象的对称性问题.同时也考查了原函数与反函数图象的对称性.