
94.证明:(1)设-1<x1<x2
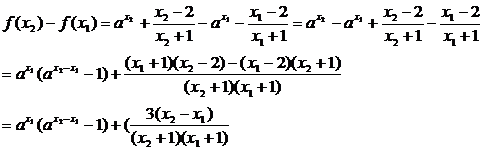
因为x2-x1>0,又a>1,所以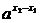 >1,而-1<x1<x2,所以x1+1>0,x2+1>0,所以f(x2)-f(x1)>0,∴f(x)在(-1,+∞)上为增函数
>1,而-1<x1<x2,所以x1+1>0,x2+1>0,所以f(x2)-f(x1)>0,∴f(x)在(-1,+∞)上为增函数
(2)设x0为方程f(x)=0的负根,则有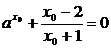 .
.
即
显然x0≠-1
当0>x0>-1时,1>x0+1>0,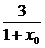 >3,-1+
>3,-1+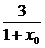 >2
>2
而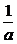 <
<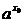 <1,这是不可能的,即不存在0>x0>-1的解
<1,这是不可能的,即不存在0>x0>-1的解
x0<-1时,x0+1<0,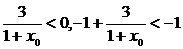
而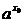 >0,矛盾,即不存在x0<-1的解.
>0,矛盾,即不存在x0<-1的解.
综上,即不存在负根
93.解:(1)f(x)=x2-x-3,因为x0为不动点,因此有f(x0)=x02-x0-3=x0
所以x0=-1或x0=3,所以3和-1为f(x)的不动点.
(2)因为f(x)恒有两个不动点,f(x)=ax2+(b+1)x+(b-1)=x,ax2+bx+(b-1)=0(※),由题设b2-4a(b-1)>0恒成立,即对于任意b∈R,b2-4ab+4a>0恒成立,所以有(4a)2-4(4a)<0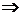 a2-a<0,所以0<a<1.
a2-a<0,所以0<a<1.
(3)由(※)式,得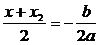 ,由题设k=-1,即y=-x+
,由题设k=-1,即y=-x+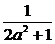 ,设A、B的中点为E,则E(
,设A、B的中点为E,则E(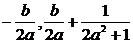 ),因为xE=yE,所以-
),因为xE=yE,所以-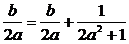
所以有b=-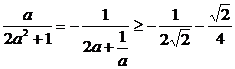 ,因为0<a<1.当且仅当2a=
,因为0<a<1.当且仅当2a=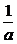 时,即a=
时,即a= 时,b取得最小值,其最小值为-
时,b取得最小值,其最小值为-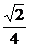 .
.
92.解:f(x)在(-∞,0)上是增函数,证明如下:
设x1<x2<0,因为f(x)为偶函数
所以f(-x1)=f(x1),f(-x2)=f(x2) ①
由设可知-x1>-x2>0,
又f(x)在(0,+∞)上是减函数于是有f(-x1)<f(-x2) ②
把①代入②得f(x1)<f(x2)
由此可得f(x)在(-∞,0)上是增函数
91.解:(1)∵函数f(x)的定义域(-∞,0)∪(0,+∞)关于原点对称,又f(-x)=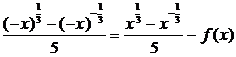 .
.
∴f(x)是奇函数.
设x1<x2,x1,x2∈(0,+∞),f(x1)-f(x2)=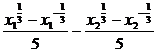
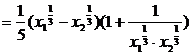 .
.
∵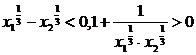 ,
,
∴f(x1)-f(x2)<0.∴f(x)在(0,+∞)上单调递增.又f(x)是奇函数,∴f(x)在(-∞,0)上也是单调递增.∴f(x)的单调区间为(-∞,0)和(0,+∞).
(2)算得f(4)-5f(2)·g(2)=0,f(9)-5f(3)·g(3)=0.由此概括出对所有不等于零的实数x有:f(x2)-5f(x)·g(x)=0.因为:f(x2)-5f(x)·g(x)=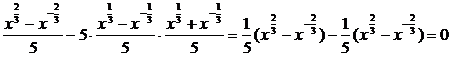 .
.
89.解:原不等式变形为:log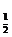 (x2-x-2)>log
(x2-x-2)>log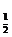 (2x-2).所以,原不等式
(2x-2).所以,原不等式
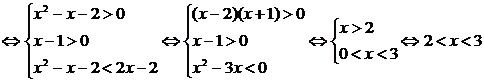
故原不等式的解集为{x|2<x<3}.
评述:本题通过对数恒等变形,转化为函数单调性问题,考查了考生的演绎推理和逻辑思维及计算能力.
※90.解:(1)当每辆车的月租金定为3600元时,未租出的车辆数为: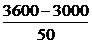 =12,所以这时租出了88辆车.
=12,所以这时租出了88辆车.
(2)设每辆车的月租金定为x元,则租赁公司的月收益为:f(x)=(100-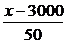 )(x-150)-
)(x-150)-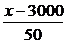 ×50,整理得:f(x)=-
×50,整理得:f(x)=-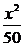 +162x-21000=-
+162x-21000=-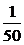 (x-4050)2+307050.所以,当x=4050时,f(x)最大,其最大值为f(4050)=307050.即当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大收益为307050元.
(x-4050)2+307050.所以,当x=4050时,f(x)最大,其最大值为f(4050)=307050.即当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大收益为307050元.
评述:本题贴近生活.要求考生读懂题目,迅速准确建立数学模型,把实际问题转化为数学问题并加以解决.
88.答案:x=4
解析:由已知得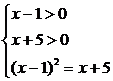 解之得x=4.
解之得x=4.
87.答案:y=-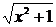 (x≥0)
(x≥0)
解析:函数的定义域x≤-1,值域y≥0,由y=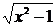 解出x,得x=-
解出x,得x=-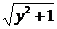 (y≥0),将x与y对换便得f-1(x)=-
(y≥0),将x与y对换便得f-1(x)=-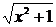 (x≥0).
(x≥0).
84.答案: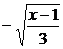 x≥1
x≥1
解析:因x≤0,所以x2≥0,3x2+1≥1,即y≥1,又由x≤0及y=3x2+1求得x=-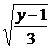 (y≥1),故所求函数的反函数为y=
(y≥1),故所求函数的反函数为y=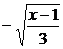 .
.
83.答案:3
解析:原方程可变形为log4(x+1)4+log4(x+1)=5,log4(x+1)5=5,
则5log4(x+1)=5,log4(x+1)=1.解得x=3,经检验x=3是方程的解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com