
3.(2008淅江金华)在a2□4a□4空格□中,任意填上“+”或“-”,在所得到的这代数式中,以构成完全平方式的概率是( )
A、1 B、1/2 C、1/3 D、1/4
2. (2008年浙江省衢州市)某校准备组织师生观看北京奥运会球类比赛,在不同时间段里有3场比赛,其中2场是乒乓球比赛,1场是羽毛球比赛,从中任意选看2场,则选看的2场恰好都是乒乓球比赛的概率是( )
A、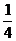 B、
B、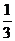 C、
C、 D、
D、
1.(2008年四川省宜宾市)一个口袋中装有4个红球,3个绿球,2个黄球,每个球除颜色外其它都相同,搅均后随机地从中摸出一个球是绿球的概率是 ( )
A. 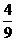 B.
B.
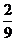 C.
C.
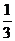 D.
D.

8.要认真准备应用题型、探索题型和综合题型,要加大训练力度.要重视关于一次函数、二次函数、对数函数的综合题型,重视关于函数的数学建模问题,重视代数与解析几何的综合题型,重视函数在经济活动和生活实际中的应用问题,学会用数学思想和方法寻求规律找出解题策略.
对函数有关概念,只有做到准确、深刻地理解,才能正确、灵活地加以运用.函数是数学中最重要的概念之一,它贯穿中学代数的始终.数、式、方程、不等式、数列及极限等,是以函数为中心的代数,高考考查的内容,几乎覆盖了中学阶段的所有函数,如一次函数、二次函数、反比例函数、指数、对数函数,还有三角函数、反三角函数等,也涉及到函数的所有主要的性质,且以考查三基为主,通性通法为主,因此更应加强函数与三角函数、不等式、数列等各章间知识的联系,养成自觉运用函数观点处理问题的习惯和培养自身的能力.
所谓函数观点,实质是将问题放到动态背景上去考虑,利用函数观点可以从较高的角度处理式、方程、不等式、数列、曲线等问题.
函数是用以描述客观世界中量的依存关系的数学概念,函数思想的实质就是用联系、变化的观点提出数学对象,建立函数关系,求得问题解决.近几年高考中,考查函数的思想方法已更加突出,特别是1993年开始考查应用题以来,考查力度逐年加大,都需用到函数的知识与方法才能解决,从如何建立函数关系式入手,考查函数的基本性质,以及数形结合、分类讨论、最优化等数学思想,重视对实践能力的考查是高考的新动向.因此要强化函数思想的应用意识的训练,才能适应高考新的变化.
7.理解掌握常见题的解题方法和思路,构建思维模式,并以此为基础进行转化发展,即在造就思维依托的基础上,还要打破框框,发展能力.
6.本章内容在高考解答题中,文科大多以对数函数为背景,结合对数运算,以考查对数函数的性质及图象等题型为主;理科解答题多以方程或二次函数为背景,综合考查函数、方程和不等式的知识,重视代数推理能力.此类试题,一般要经过变形转化,归结为二次函数问题解决.这是近年高考的重点和热点.在此基础上,理解和掌握常见的平移、对称变换方法.以基本函数为基础,强化由式到图和由图到式的转化训练.
加强函数思想、转化思想的训练是本章复习的另一个重点.善于转化命题,引进变量建立函数,运用变化的方法、观点解决数学试题以提高数学意识,发展能力.
5.与映射有关的试题:1998年以前的全国试题均没有涉及映射的概念,在1999年和2000年连续两年考查了映射的概念,说明尽管《考试说明》中对映射的要求不高,但在高考中有加强的趋势,我们在复习中要予以重视.在映射问题中,有许多的题目叙述是映射,实际问题是函数,因为数集到数集的映射即为函数.
4.与指数函数和对数函数有关的试题.对指数函数与对数函数的考查,大多以基本函数的性质为依托,结合运算推理来解决.能运用性质比较熟练地进行大小的比较、方程的求解等.会利用基本的指数函数或对数函数的性质研究简单复合函数的单调性、奇偶性等性质,熟练掌握指数、对数运算法则,明确算理,能对常见的指数型函数、对数型函数进行变形处理.
3.与反函数有关的试题,大多是求函数的解析式,定义域、值域或函数图象等,一般不需求出反函数,只需将问题转化为与原函数有关的问题即可解决.
2.与函数图象有关的试题,要从图中(或列表中)读取各种信息,注意利用平移变换、伸缩变换、对称变换,注意函数的对称性、函数值的变化趋势,培养运用数形结合思想来解题的能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com