98.(2002北京理，22)已知f(x)是定义在R上的不恒为零的函数，且对于任意的a，b∈R都满足：f(a·b)=af(b)+bf(a).

(1)求f(0)，f(1)的值；

(2)判断f(x)的奇偶性，并证明你的结论；

(3)f(2)=2，u_n=(n∈N)，求数列{u_n}的前n项的和S_n.

97.(2002北京文，22)已知f(x)是定义在R上的不恒为零的函数，且对于任意的a，b∈R都满足：f(a·b)=af(b)+bf(a).

(1)求f(0)，f(1)的值；

(2)判断f(x)的奇偶性，并证明你的结论；

(3)若f(2)=2，u_n=f(2ⁿ)(n∈N)，求证：u_n+1＞u_n(n∈N).

96.(2002全国理，21)设a为实数，函数f(x)=x²+|x－a|+1，x∈R.

(1)讨论f(x)的奇偶性；

(2)求f(x)的最小值.

95.(2002全国文，20)设函数f(x)=x²+|x－2|－1，x∈R.

(1)判断函数f(x)的奇偶性；

(2)求函数f(x)的最小值.

94.(2002上海春，20)已知函数f(x)=a^x+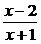(a＞1).

(1)证明：函数f(x)在(－1，+∞)上为增函数；

(2)用反证法证明方程f(x)=0没有负数根.

93.(2002京、皖春，22)对于函数f(x)，若存在x₀∈R，使f(x₀)=x₀成立，则称x₀为f(x)的不动点.

已知函数f(x)=ax²+(b+1)x+(b－1)(a≠0).

(1)当a=1，b=－2时，求函数f(x)的不动点；

(2)若对任意实数b，函数f(x)恒有两个相异的不动点，求a的取值范围；

(3)在(2)的条件下，若y=f(x)图象上A、B两点的横坐标是函数f(x)的不动点，且A、B两点关于直线y=kx+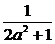对称，求b的最小值.

92.(2002京、皖春，18)已知f(x)是偶函数，而且在(0，+∞)上是减函数，判断f(x)在(－∞，0)上是增函数还是减函数，并加以证明.

91.(2003上海春，20)已知函数.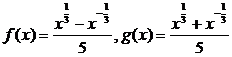

(1)证明f(x)是奇函数；并求f(x)的单调区间.

(2)分别计算f(4)－5f(2)g(2)和f(9)－5f(3)g(3)的值，由此概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式，并加以证明.

89.(2003北京春，17)解不等式：log₂(x²－x－2)>log₂(2x－2).

^※90.(2003北京春，理、文21)某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时，可全部租出.当每辆车的月租金每增加50元时，未租出的车将会增加一辆.租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元.

(1)当每辆车的月租金定为3600元时，能租出多少辆车？

(2)当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？

88.(1994上海，4)方程log₃(x－1)＝log₉(x+5)的解是　　　　　 .