
1.
C 解析: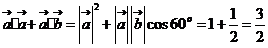 .
.
4.
解析:(1)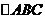 的内角和
的内角和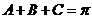 ,由
,由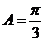 ,
,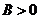 ,
,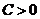 得
得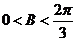 .
.
应用正弦定理,知:
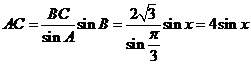
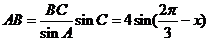
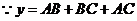
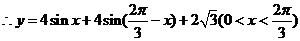
(2)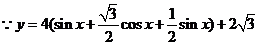
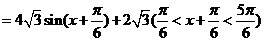
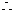 当
当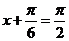 ,即
,即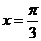 时,
时,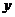 取得最大值
取得最大值 .
.
3.
解:(1)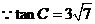 ,
,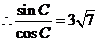 .
.
又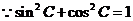 ,解得
,解得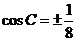 .
.
 ,
,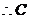 是锐角.
是锐角.  .
.
(2)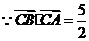 .
. 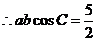 .
. 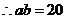 .
.
又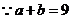 ,
,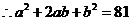 .
. 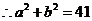 .
.
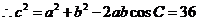 .
. 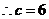 .
.
2.
C 解析: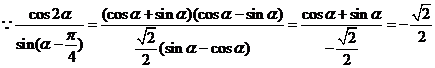
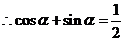
1.
A 解析: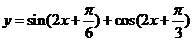
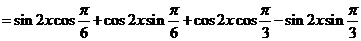
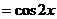
 ,
,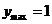 .
.
6. (1)经计算可得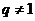 ,由等比数列前n项和公式得
,由等比数列前n项和公式得
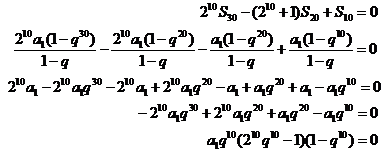
因为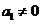 ,
,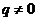 ,
,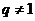 ,因此以上方程的解为
,因此以上方程的解为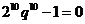 ,即
,即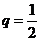 .
.
因此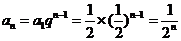 (此通项也适合
(此通项也适合 )
)
(2)由(1)的结果得:
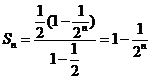
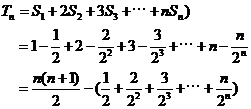
令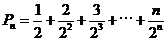 ,则
,则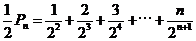
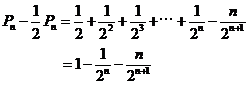
因此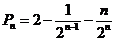 ,
,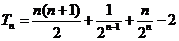
5. (1)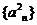 的公比为
的公比为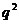 ,由公比
,由公比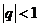 的无穷等比数列求和公式
的无穷等比数列求和公式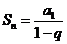 得:
得:
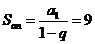 ,
, 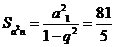 ,解得:
,解得: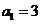 ,
,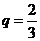 ;
;
(2)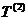 的首项为
的首项为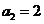 ,公差为
,公差为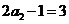 ,
,
因此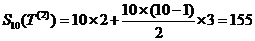 ;
;
(3)先求出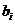 的表达式,
的表达式,
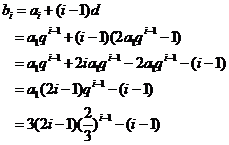
把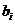 看成
看成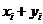 ,其中
,其中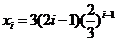 ,
,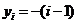 ,则
,则
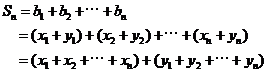
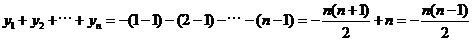
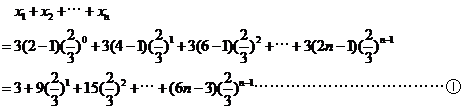
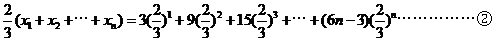
由 得:
得:
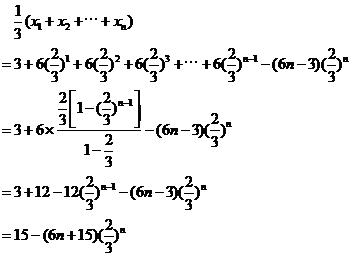
因此: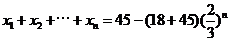
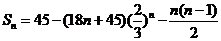
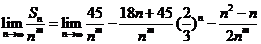 ,
,
当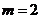 时,
时,
当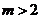 时,
时,
因此,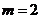 .
.
4. (1)利用等差中项的性质得出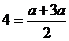 ,解得
,解得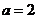 ,
,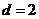 再利用求和公式
再利用求和公式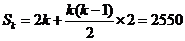 解得
解得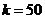 .
.
(2)由(1)的结果可知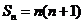 ,因此原极限可化为:
,因此原极限可化为:
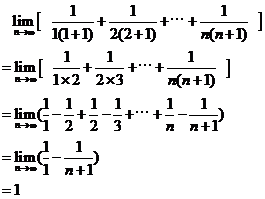
3. 根据等比数列补充性质可得插入的中间数为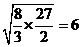 ,因此由等比中项得此3数的积为
,因此由等比中项得此3数的积为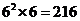 .
.
2. 由等差中项性质可得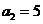 ,代入可求出
,代入可求出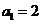 ,
,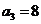 ;
;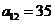 ,因此
,因此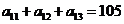 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com