
1. 偶数项之和减去奇数项之和等于5d,因此d=3.
6.
若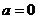 ,则函数
,则函数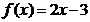 在区间
在区间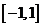 上没有零点.
上没有零点.
当 时分3种情况讨论.
时分3种情况讨论.
(1)
方程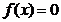 在区间
在区间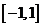 上有重复的根,此时
上有重复的根,此时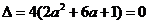 ,
,
解得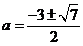 ,代入解得
,代入解得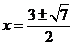 ,因为
,因为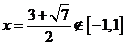 舍去,
舍去,
因此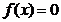 在区间
在区间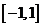 上有重根时,
上有重根时,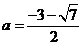 .
.
(2)
方程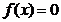 在区间
在区间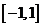 上只有一个零点且不是
上只有一个零点且不是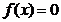 的重根.
的重根.
此时有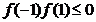 .
.
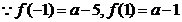
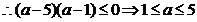
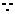 当
当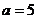 时,方程
时,方程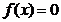 在区间
在区间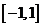 有两个相异实根.
有两个相异实根.
故当方程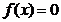 在区间
在区间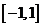 上只有一个零点且不是重根时,
上只有一个零点且不是重根时,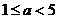 .
.
(3)
方程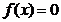 在区间
在区间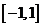 上有两个相异实根.
上有两个相异实根.
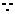 函数
函数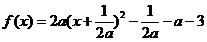 ,其图像的对称轴方程为
,其图像的对称轴方程为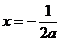 ,
, 应满足:
应满足: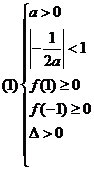 或
或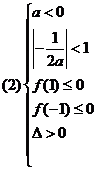
解(1)得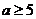 ;解(2)得
;解(2)得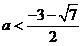
故当方程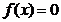 在区间
在区间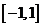 上有两个相异实根时,
上有两个相异实根时,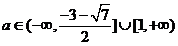
综上所述,函数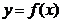 在区间
在区间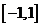 上有零点,则
上有零点,则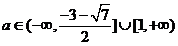 .
.
5.
(1)由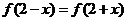 ,
,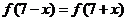 得函数
得函数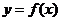 得对称轴为
得对称轴为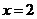 和
和 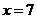 . 从而知函数
. 从而知函数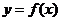 不是奇函数;又
不是奇函数;又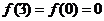 ,而
,而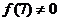 ,故函数
,故函数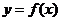 是非奇非偶函数.
是非奇非偶函数.
(2)由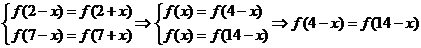 可得
可得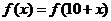 ,从而知函数
,从而知函数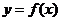 得周期为T=10.
得周期为T=10.
又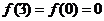 ,
,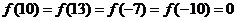 ,故
,故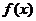 在
在 和
和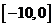 上均有两个解,从而可知在
上均有两个解,从而可知在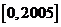 上有402个解,在
上有402个解,在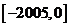 上有400个解,因此
上有400个解,因此 在
在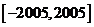 上有802个解.
上有802个解.
4.
因为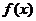 定义域为R,所以
定义域为R,所以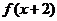 是定义域为R的奇函数,图像必过原点. 将其图像向右平移2个单位后得到函数
是定义域为R的奇函数,图像必过原点. 将其图像向右平移2个单位后得到函数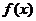 图像,且知
图像,且知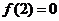 ,函数
,函数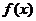 图像关于点
图像关于点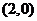 对称.
对称.
已知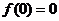 ,所以
,所以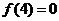 即
即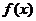 的图像与x轴交3点.
的图像与x轴交3点.
又已知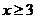 ,
,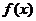 递增,所以当
递增,所以当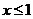 时,
时,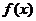 递增.
递增.
故知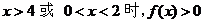 ;
;
因此满足条件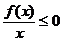 的x的取值范围
的x的取值范围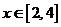
3.
设函数 ,作其图像,如右图所示,曲线C是两抛物线的部分图形,关于y轴对称. 很明显,当
,作其图像,如右图所示,曲线C是两抛物线的部分图形,关于y轴对称. 很明显,当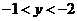 时,直线L与曲线C有4个交点,故m的取值范围为
时,直线L与曲线C有4个交点,故m的取值范围为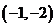 .
.
2.
D 解析:由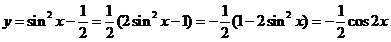
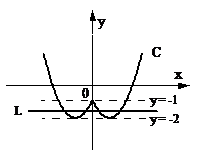
 ,且
,且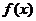 是偶函数.
是偶函数.
1.
C 解析: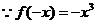 ,
,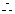 是单调递减的奇函数.
是单调递减的奇函数.
5. 设全集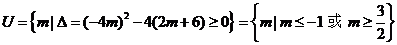 ,若原方程两根非负,则须
,若原方程两根非负,则须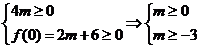 ,因此
,因此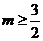 .
.
故它在全集U下的补集为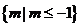 即为所求m的范围.
即为所求m的范围.
4. 如右图所示,可知集合Q的补集为阴影部分,即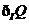 ,
,
显然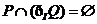
3. 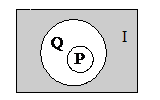 B
解析:
B
解析: ,故
,故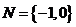 ,
,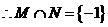 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com