
6. 用通项公式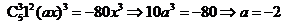 .
.
5. 目标被命中的对立事件是目标不被命中,其概率为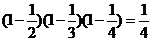 ,所以目标被命中的概率为
,所以目标被命中的概率为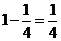 ,3人同时命中的概率为
,3人同时命中的概率为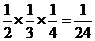 .
.
4. 直接计算比较麻烦,可先求出任选两把不能开锁的总数,再由基本事件减去这个情况就为能够开锁的情况,即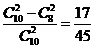 .
.
3. 先让甲工程队选择,再让其4个工程队任选,即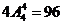 种.
种.
2. 因为三个学校分别有1,1,2个老师,所以先任选出两位老师组成一组,再和其他两位分别分到3所学校,即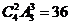 种.]
种.]
1. 将两个节目分别插入原来的5节目中,则第一个节目有6个选择,插入后第二个节目有7个选择,因此不同的插法有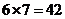 种.
种.
3.(1) ,
,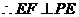
又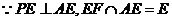 ,且
,且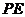 在平面
在平面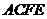 外,
外,
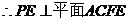 .
.
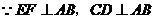 ,
,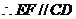 ,
,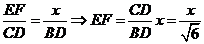
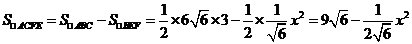
 四棱锥
四棱锥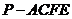 的体积
的体积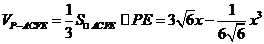
即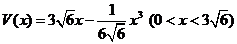
(2)由(1)知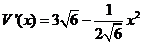 ,令
,令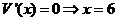

 当
当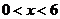 时,
时,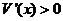 ;当
;当 时,
时,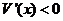 .
.
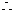 当
当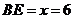 时,
时,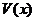 取得最大值
取得最大值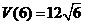
(3)过点F作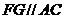 交
交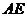 于点G,连接
于点G,连接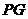 ,
,
则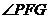 为异面直线
为异面直线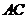 与
与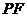 所成的角.
所成的角.
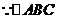 是等腰三角形
是等腰三角形
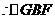 也是等腰三角形
也是等腰三角形
于是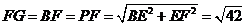
从而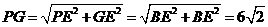 .
.
在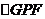 中,根据余弦定理得
中,根据余弦定理得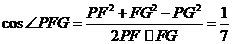 .
.
故异面直线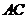 与
与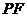 所成角的余弦值为
所成角的余弦值为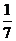 .
.
2.由题设可知几何体是一个高为4的四棱锥,底面是长、宽分别为8、6的矩形;正侧面是底为8,高为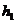 的等腰三角形;左侧面是底为6,高为
的等腰三角形;左侧面是底为6,高为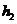 的等腰三角形. 如有图所示.
的等腰三角形. 如有图所示.
(1) 几何体的体积为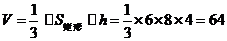 .
.
(2) 正侧面底边上的高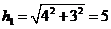 ;左侧面底边上的高
;左侧面底边上的高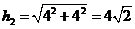
因此几何体的侧面积为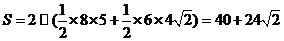
1.解析:所有顶点确定的直线共有:棱数+底边数+对角线数,即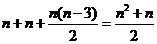
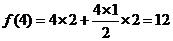

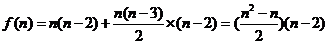
3.
(1)设圆C的圆心为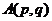 ,则圆C得方程为
,则圆C得方程为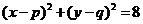 .
.
 直线
直线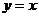 与圆C相切于坐标原点O
与圆C相切于坐标原点O
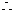 O在圆C上,且直线OA垂直于直线
O在圆C上,且直线OA垂直于直线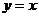 .
.
于是有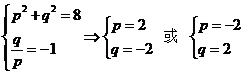
由于点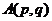 在第二象限,故
在第二象限,故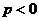 .
.
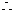 圆C得方程为
圆C得方程为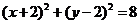
(2) 椭圆
椭圆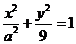 与圆C的一个交点到椭圆两焦点距离之和为10,
与圆C的一个交点到椭圆两焦点距离之和为10,
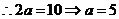 ,故椭圆右焦点为
,故椭圆右焦点为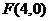
若圆C上存在异于原点的点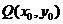 到椭圆右焦点
到椭圆右焦点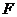 得距离等于线段OF的长,则有
得距离等于线段OF的长,则有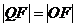 ,于是
,于是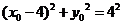 ,且
,且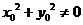
由于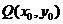 在圆上,故有
在圆上,故有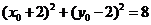 ,解得
,解得
故圆C上存在满足条件的点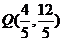 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com