
3.给出下列命题:
①若平面α的两条斜线段PA、PB在α内的射影长相等,那么PA、PB的长度相等;
②已知PO是平面α的斜线段,AO是PO在平面α内的射影,若OQ⊥OP,则必有OQ⊥OA;
③与两条异面直线都平行的平面有且只有一个;
④平面α内有两条直线a、b都与另一个平面β平行,则α∥β.
上述命题中不正确的是 ( )
A.①②③④ B.①②③ C.①③④ D.②③④
2.下列命题中正确的是 ( )
A.过平面外一点作这个平面的垂面有且只有一个
B.过直线外一点作这条直线的平行平面有且只有一个
C.过直线外一点作这条直线的垂线有且只有一条
D.过平面的一条斜线作这个平面的垂面有且只有一个
1.若两直线a⊥b,且a⊥平面a,则b与a的位置关系
是 ( )
A、相交 B、b∥a C、b∥a,或bÌa D、bÌa
3.线面角的求法:作出射影转化为平面内的角.
同步练习 9.3线面垂直、三垂线定理
[选择题]
2.证明线面垂直的常用方法:
(1)用判定定理;
(2)与直线的垂面平行
(3)用面面垂直的性质定理;
(4)同一法.
(5)用活三垂线定理证线线垂直.
1.熟练掌握线面垂直的判定定理及性质定理.
[例1]AD为△ABC中BC边上的高,在AD上取一点E,使AE=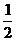 DE,过E点作直线MN∥BC,交AB于M,交AC于N,现将△AMN沿MN折起,这时A点到A¢点的位置,且ÐA¢ED=60°,求证:A¢E⊥平面A¢BC.
DE,过E点作直线MN∥BC,交AB于M,交AC于N,现将△AMN沿MN折起,这时A点到A¢点的位置,且ÐA¢ED=60°,求证:A¢E⊥平面A¢BC.
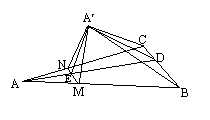
 [例2]如图,P为△ABC所在平面外一点,PA⊥平
[例2]如图,P为△ABC所在平面外一点,PA⊥平
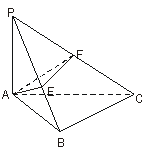 面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,
面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,
求证:
(1)BC⊥平面PAB;
(2)AE⊥平面PBC;
(3)PC⊥平面AEF.
证明:(1)PA⊥平面ABC
|
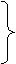 PA⊥BC
PA⊥BC
AB⊥BC
PA∩AB=A
(2)AE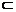 平面PAB,
平面PAB,
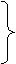
|
AE⊥PB
PB∩BC=B
(3)PC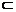 平面PBC,
平面PBC,
|
PC⊥AF
AE∩AF=A
[例3]如图,直三棱柱ABC-A1B1C1中,ÐACB=90°,AC=1,CB=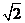 ,侧棱AA1=1,侧面A A1 B1B的两条对角线交于点D,B1C1的中点为M,
,侧棱AA1=1,侧面A A1 B1B的两条对角线交于点D,B1C1的中点为M,
求证:CD^平面BDM

证明:在直三棱柱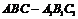 中
中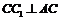 ,又
,又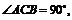
∴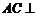 平面
平面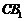 ,
,
∵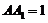 ,
,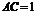 ∴
∴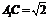 ,
,
∴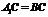 ,
, 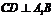
连结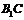 ,则
,则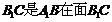 上的射影,也是CD的射影
上的射影,也是CD的射影
在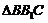 中,
中,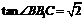
在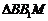 中,
中,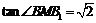 ,
,
∴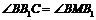 , ∴
, ∴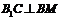 ,
,
∴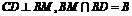 ,
,
∴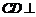 平面
平面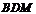 .
.
◆总结提练: 证线面垂直, 要注意线线垂直与线面垂直关系与它之间的相互转化
证线线垂直常用余弦定理、勾股定理逆定理,三垂线定理或通过线面垂直.
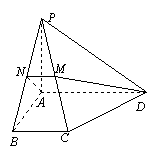
[例4](2006浙江)如图,在四棱锥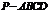 中,底面为直角梯形,
中,底面为直角梯形,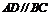 ,
,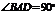 ,
,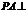 底面
底面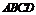 ,
,
且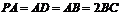 ,
,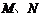 分别为
分别为 、
、 的中点.
的中点.
(Ⅰ)求证: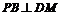 ;
;
(Ⅱ)求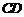 与平面
与平面 所成的角.
所成的角.
解:(I)∵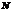 是
是 的中点,
的中点,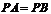 ,∴
,∴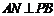 .
.
∵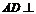 平面
平面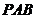 ,∴
,∴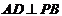 ,从而
,从而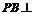 平面
平面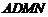 .
.
∵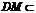 平面
平面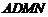 ,∴
,∴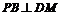 .
.
(II)取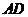 的中点
的中点 ,连结
,连结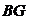 、
、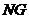 ,则
,则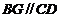 ,
,
∴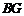 与平面
与平面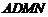 所成的角和
所成的角和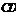 与面
与面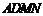 所成的角相等.
所成的角相等.
∵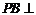 平面
平面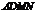 ,
,
∴NG是BG在面ADMN内的射影,
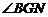 是
是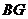 与平面
与平面 所成的角.
所成的角.
在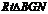 中,
中,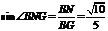 .
.
故 与平面
与平面 所成的角是
所成的角是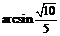 .
.
6. 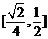 .CD⊥平面α时射影面积最小
.CD⊥平面α时射影面积最小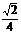 ;CD//α时射影面积最大
;CD//α时射影面积最大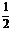 .
.
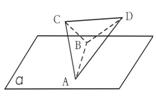
6.(2006浙江)正四面体ABCD的棱长为l,棱AB∥平面 ,则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是______.
,则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是______.
◆答案提示:1-3.DBDA; 5. a∥d;
5.直线a,b,c 是两两互相垂直的异面直线,直线 d是b和c的公垂线,则d和a 的位置关系是______________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com