14. (1)解法一(树状图)

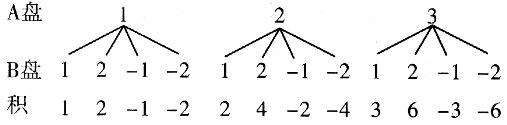
从上图可以看出，共有12种可能结果，其中是奇数的有4种可能结果，因此P(甲胜)=。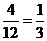

解法二(列表法)

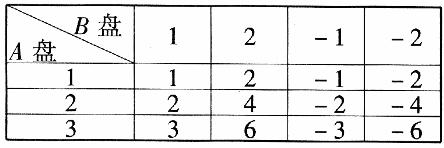
(以下过程同“解法一”)

(2)不公平。

P(甲胜)=，P(乙胜)=。

13.　 (1)x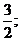＜………………………………………………………………………………3分

　在数轴上正确表示此不等式的解集(略)……………………………………………4分

　　(2)用列举法

　　　 取a=－1，不等式ax+3＞0的解为x＜3，不等式有正整数解.

　　取a=－2，不等式ax+3＞0的解为x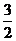＜,不等式有正整数解.……………………6分

取a=－3，不等式ax+3＞0的解为x＜1，不等多没有正整数解.

　　取a=－4，不等式ax+3＞0的解为x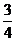＜,不等式没有正整数解.

　　……

∴整数a取－3至－10中任意一个整数时，不等式没有正整数解.………………8分

P(不等式没有正整数解)=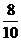=　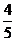 …………………………10分

12. (1) 出现和为7的概率是：0.33(或0.31， 0.32，0.34均正确)

(2) 列表格(见右边)或树状图，一共有12种可能的结果,

由(1)知，出现和为7的概率约为0.33

∴和为7出现的次数为0.33×12=3.96≈4(用另外三个概率估计值说明亦可)

若2+x=7,则x=5,此时P(和为7)=≈0.33,　 符合题意.

若3+x=7,则 x=4,不符合题意.

若4+x=7,则 x=3,不符合题意.

所以x=5.　　

(说理方法多种，只要说理、结果正确均可)

11. (1)P(取到欢欢)=；

(2)列表如下：

第二次 第一次	贝	晶	欢	迎	妮
贝	-　 -	贝、晶	贝、欢	贝、迎	贝、妮
晶	晶、贝	-　 -	晶、欢	晶、迎	晶、妮
欢	欢、贝	欢、晶	-　 -	欢、迎	欢、妮
迎	迎、贝	迎、晶	迎、欢	-　 -	迎、妮
妮	妮、贝	妮、晶	妮、欢	妮、迎	-　 -

树形图如下：

由表(图)可知：P(两次取到“贝贝”、“晶晶”)=。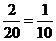

10. 解：将两次摸乒乓球可能出现的结果列表如下：

第 一次 第二次	1	2	3	4
1	(1，1)	(1，2)	(1，3)	(1，4)
2	(2，1)	(2，2)	(2，3)	(2，4)
3	(3，1)	(3，2)	(3，3)	(3，4)
4	(4，1)	(4，2)	(4，3)	(4，4)

以上共有16种等可能结果

两次摸出乒乓球标号相同的结果有4种.

故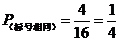

两次摸出的乒乓球的标号的和等于5的结果有4种，

　故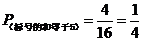

9. 乙获胜的可能性大。

进行一次游戏所有可能出现的结果如下表：

从表上可以看出，一次游戏可能出现的结果共有16种，而且每种结果出现的可能性相等，其中两次取出的牌中都没有K的有(J，J)，(J，Q)，(Q，J)，(Q，Q)等4种结果。

∴P(两次取出的牌中都没有K)=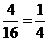。∴P(甲获胜)=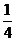，P(乙获胜)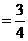。故乙获胜的可能性大。

8. 解：(1)设红球的个数为，

　　 由题意得，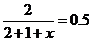

　　 解得， .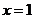

　　 答：口袋中红球的个数是1.

　 (2)小明的认为不对.

　　 树状图如下：

　　

∴ ，，.

∴　 小明的认为不对.

7. 解(1)x=35(2)900×45%=405

(3)所有可能情况:篮1篮2,篮1篮3, 篮1乒,篮1足,篮2篮3,篮2乒,篮2足,篮3乒,篮3足,乒足共10种情况.

P(2人均是最喜欢篮球运动的学生)=

6. 解：(1)从纸箱中随机地一次取出两个小球，所标数字的所有可能结果有：

(1，2)、(1，3)、(1，4)、(2，3)、(2，4)、(3，4)，共6种；

　而所标数字一个是奇数另一个是偶数的有4种。 　　　　　　　　　　　……3分

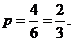∴　　　　　　　　　　　　　　　　　　　　　　　　　　 ……2分

(2)画树状图：

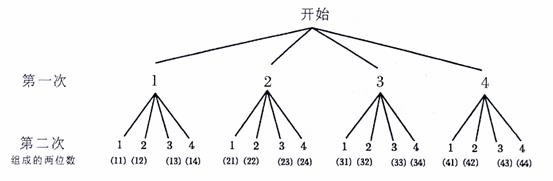
或用列表法

第二次 第一次	1	2	3	4
1	(11)	(12)	(13)	(14)
2	(21)	(22)	(23)	(24)
3	(31)	(32)	(33)	(34)
4	(41)	(42)	(43)	(44)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……3分

　　　 所有可能出现的结果共有16种，其中能被3整除的有5种。

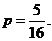　　　　　 ∴　　　　　　　　　　　　　　　　　　　　　 ……2分

5. 解：(1)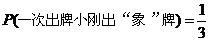····························································· 4分

(2)树状图(树形图)：

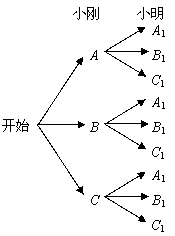
·························································································· 8分

或列表

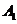
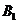
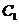
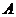
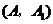
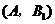
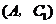
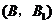
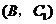
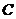
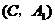
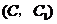
　　　　　　　　　　　　　　　　　　 ······································································ 8分

由树状图(树形图)或列表可知，可能出现的结果有9种，而且每种结果出现的可能性相同，其中小刚胜小明的结果有3种．······························································································································ 9分

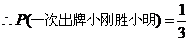．　　 10分