111.(2000上海春，17)设f(x)为定义在R上的偶函数，当

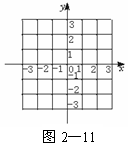
x≤－1时，y＝f(x)的图象是经过点(－2，0)，斜率为1的射线，又在y＝f(x)的图象中有一部分是顶点在(0，2)，且过点(－1，1)的一段抛物线.试写出函数f(x)的表达式，并作出其图象.

110.(2000春季北京安徽理，21)设函数f(x)＝|lgx|，若0＜a＜b，且f(a)＞f(b)，

证明：ab＜1．

109.(2000春季北京、安徽文，19)已知二次函数f(x)＝(lga)x²+2x+4lga的最大值为3，求a的值.

107.(2001天津，19)设a＞0，f(x)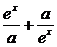＝是R上的偶函数.

(1)求a的值；

(2)证明f(x)在(0，+∞)上是增函数．

^※108.(2000全国，21)某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿市场售价与上市时间的关系用图2-10中(1)的一条折线表示；西红柿的种植成本与上市时间的关系用图2-10中(2)的抛物线表示.

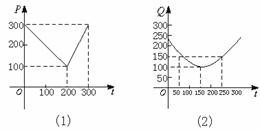
图2-10

(1)写出图中(1)表示的市场售价与时间的函数关系式P＝f(t)；

写出图中(2)表示的种植成本与时间的函数关系式Q＝g(t)；

(2)认定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大?

(注：市场售价和种植成本的单位：元／10² ，kg，时间单位：天)

105.(2001春季北京、安徽，12)设函数f(x)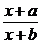＝(a＞b＞0)，求f(x)的单调区间，并证明f(x)在其单调区间上的单调性.

^※106.(2001上海，文、理21)用水清洗一堆蔬菜上残留的农药．对用一定量的水清洗一次的效果作如下假定：用1个单位量的水可洗掉蔬菜上残留农药量的，用水越多洗掉的农药量也越多，但总还有农药残留在蔬菜上．设用x单位量的水清洗一次以后，蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数f(x).

(1)试规定f(0)的值，并解释其实际意义；

(2)试根据假定写出函数f(x)应该满足的条件和具有的性质；

(3)设f(x)=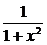，现有a(a＞0)单位量的水，可以清洗一次，也

可以把水平均分成2份后清洗两次，试问用哪种方案清洗后蔬菜上残留的农药量比较少?说明理由．

103.(2001全国理，22)设f(x)是定义在R上的偶函数，其图象关于直线x＝1对称，对任意x₁，x₂∈［0，］，都有f(x₁+x₂)＝f(x₁)·f(x₂)，且f(1)＝a＞0.

(1)求f()及f()；

(2)证明f(x)是周期函数；

(3)a_n＝f(2n+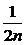)，求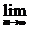(lna_n).

^※104.(2001全国文，21)设计一幅宣传画，要求画面面积为4840 cm²，画面的宽与高的比为λ(λ＜1，画面的上、下各留8 cm空白，左、右各留5 cm空白.怎样确定画面的高与宽尺寸，能使宣传画所用纸张面积最小?

102.(2001全国文，22)设f(x)是定义在R上的偶函数，其图象关于直线x＝1对称，对任意x₁，x₂∈［0，］，都有f(x₁+x₂)＝f(x₁)·f(x₂).

(1)设f(1)＝2，求f()，f()；

(2)证明f(x)是周期函数；

101.(2002河南、广东、广西，22)已知a>0，函数f(x)=ax－bx².

(1)当b>0时，若对任意x∈R都有f(x)≤1，证明a≤2；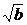

(2)当b>1时，证明：对任意x∈［0，1］，|f(x)|≤1的充要条件是b－1≤a≤2；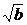

(3)当0<b≤1时，讨论：对任意x∈［0，1］，|f(x)|≤1的充要条件.

100.(2002上海理，19)已知函数f(x)=x²+2x·tanθ－1，x∈［－1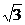，］，其中θ∈(－).

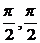(1)当θ=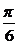－时，求函数f(x)的最大值与最小值；

(2)求θ的取值范围，使y=f(x)在区间［－1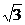，］上是单调函数.

99.(2002上海文，19)已知函数f(x)=x²+2ax+2，x∈［－5，5］

(1)当a=－1时，求函数f(x)的最大值和最小值；

(2)求实数a的取值范围，使y=f(x)在区间［－5，5］上是单调函数.