
1. (2003高考,北京)某班新年联欢会原定的5个节目已排成节目单,开演前又增加了两个新节目,如果将这两个节目插入原节目单中,那么不同的插法有____种.
3.  (2007,广东理)如图所示,等腰
(2007,广东理)如图所示,等腰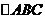 的底边
的底边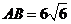 ,高
,高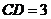 . 点E是线段B D上异于点B、D的动点. 点F在BC边上,且
. 点E是线段B D上异于点B、D的动点. 点F在BC边上,且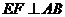 . 现沿EF将
. 现沿EF将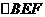 折起到
折起到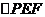 的位置,使
的位置,使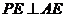 . 记
. 记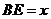 ,
,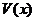 表示四棱锥
表示四棱锥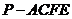 的体积.
的体积.
(1)
求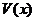 的表达式
的表达式
(2)
当x为何值时,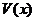 取得最大值?
取得最大值?
(3)
当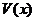 取得最大值时,求异面直线AC与PF所成角的余弦值.
取得最大值时,求异面直线AC与PF所成角的余弦值.
第九章 排列组合、二项式定理及概率统计
2.  (2007,广东文)已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.
(2007,广东文)已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.
(1) 求该几何体的体积V;
(2) 求该几何体的侧面积S.
1. (2007,广东)如果一个凸多面体是n棱锥,那么这个凸多面体的所有顶点所确定的直线共有____条. 这些直线中共有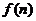 对异面直线,则
对异面直线,则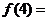 ____;
____;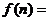 ____.
____.
3. (2007,广东)在平面直角坐标系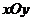 中,已知圆心在第二象限、半径为
中,已知圆心在第二象限、半径为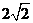 的圆C与直线
的圆C与直线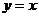 相切于坐标原点O. 椭圆
相切于坐标原点O. 椭圆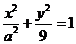 与圆C的一个交点到椭圆两焦点的距离之和为10.
与圆C的一个交点到椭圆两焦点的距离之和为10.
(1) 求圆C的方程.
(2) 试探究圆C上是否存在异于原点的点Q,使Q到椭圆右焦点F的距离等于线段OF的长. 若存在,请求出点Q的坐标;若不存在,请说明理由.
第八章 立体几何
2. (2007,广东理)在平面直角坐标系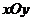 中,有一定点
中,有一定点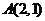 ,若线段OA的垂直平分线过抛物线
,若线段OA的垂直平分线过抛物线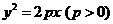 的焦点,则该抛物线的准线方程是________.
的焦点,则该抛物线的准线方程是________.
1. (2007,广东文)在平面直角坐标系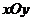 中,已知抛物线关于x轴对称,顶点在原点O,且过点
中,已知抛物线关于x轴对称,顶点在原点O,且过点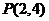 ,则该抛物线的方程是________.
,则该抛物线的方程是________.
5. 设一个三角形的三条边长为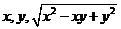 ,则最长边与最短边的夹角等于______.
,则最长边与最短边的夹角等于______.
第七章 解析几何
4. 设某直角三角形三边之和为P,则这个直角三角形的最大面积为_________.
3. 不等式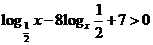 的解集是______.
的解集是______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com