
1 函数y=tan(ax+
函数y=tan(ax+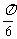 )(a≠0)的最小正周期为( )
)(a≠0)的最小正周期为( )

2 以下函数中,不是奇函数的是( )
以下函数中,不是奇函数的是( )
A y=sinx+tanx B.y=xtanx-1
C.y=
y=sinx+tanx B.y=xtanx-1
C.y=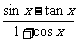 D.y=lg
D.y=lg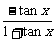
3 下列命题中正确的是( )
下列命题中正确的是( )
A.y=cosx在第二象限是减函数 B.y=tanx在定义域内是增函数
C.y=|cos(2x+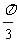 )|的周期是
)|的周期是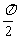 D.y=sin|x|是周期为2π的偶函数
D.y=sin|x|是周期为2π的偶函数
4 函数y=sinx+tanx,x∈[-
函数y=sinx+tanx,x∈[-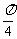 ,
,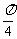 ]的值域为
]的值域为

5 函数y=cotx-tanx的周期为
函数y=cotx-tanx的周期为 
6 函数y=
函数y=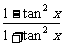 的周期为
的周期为 
7 作出函数y=|tanx|的图象,并观察函数的最小正周期和单调区间
作出函数y=|tanx|的图象,并观察函数的最小正周期和单调区间
8 试证cotx=-tan(
试证cotx=-tan(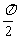 +x),并指出通过怎样的图象变换可由y=tanx的图象得到y=cotx的图象
+x),并指出通过怎样的图象变换可由y=tanx的图象得到y=cotx的图象 ?
?
9 作出函数y=
作出函数y=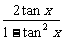 的图象,并观察函数的周期
的图象,并观察函数的周期
例1比较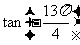 与
与 的大小
的大小
解: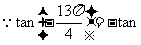
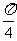 ,
,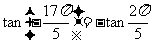 ,
,
又: 内单调递增,
内单调递增,


例2讨论函数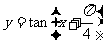 的性质
的性质
略解:定义域: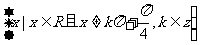
值域:R 奇偶性:非奇非偶函数
单调性:在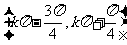 上是增函数
上是增函数
图象:可看作是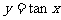 的图象向左平移
的图象向左平移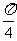 单位
单位
例3求函数y=tan2x的定义域
解:由2x≠kπ+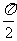 ,(k∈Z)
,(k∈Z)
得x≠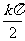 +
+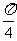 ,(k∈Z)
,(k∈Z)
∴y=tan2x的定义域为:{x|x∈R且x≠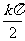 +
+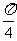 ,k∈Z}
,k∈Z}
例4观察正切曲线写出满足下列条件的x的值的范围:tanx>0
解:画出y=tanx在(-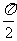 ,
,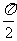 )上的图象,不难看出在此区间上满足tanx>0的x的范围为:0<x<
)上的图象,不难看出在此区间上满足tanx>0的x的范围为:0<x<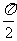
结合周期性,可知在x∈R,且x≠kπ+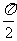 上满足的x的取值范围为(kπ,kπ+
上满足的x的取值范围为(kπ,kπ+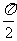 )(k∈Z)
)(k∈Z)
例5不通过求值,比较tan135°与tan138°的大小
解:∵90°<135°<138°<270°
又∵y=tanx在x∈(90°,270°)上是增函数
∴tan135°<tan138°
6.单调性:在开区间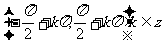 内,函数单调递增
内,函数单调递增
余切函数y=cotx的图象及其性质(要求学生了解):
 --即将
--即将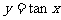 的图象,向左平移
的图象,向左平移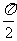 个单位,再以x轴为对称轴上下翻折,即得
个单位,再以x轴为对称轴上下翻折,即得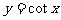 的图象
的图象
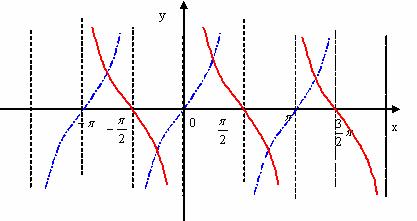 定义域:
定义域: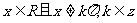
值域:R,
当 时
时 ,当
,当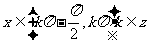 时
时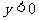
周期:
奇偶性:奇函数
单调性:在区间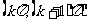 上函数单调递减
上函数单调递减
5.奇偶性: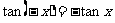 奇函数
奇函数
4.周期性:
3.观察:当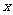 从小于
从小于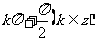 ,
,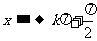 时,
时,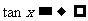
当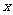 从大于
从大于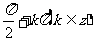 ,
,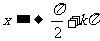 时,
时,

2.值域:R
1.定义域: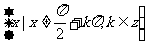 ,
,
3.因此我们可选择 的区间作出它的图象
的区间作出它的图象
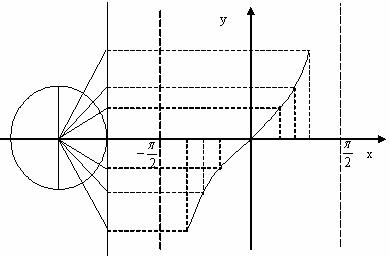
根据正切函数的周期性,把上述图象向左、右扩展,得到正切函数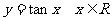 ,且
,且 的图象,称“正切曲线”
的图象,称“正切曲线”
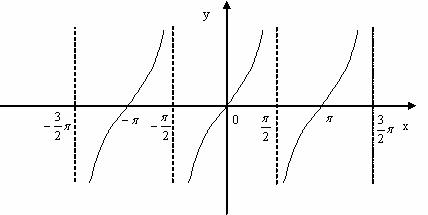
正切函数的性质:
2.为了研究方便,再考虑一下它的周期:
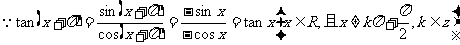
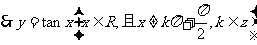 的周期为
的周期为 (最小正周期)
(最小正周期)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com