
22.①除去外力后,A以未加外力时的位置为平衡位置做简谐运动,当A运动到平衡位置上方最大位移处时,B恰好对地面压力为零,A的加速度最大,设为am,对整体由牛顿第二定律有:(M+m)g=M×0+mam
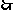 am=(M+m)g/m,方向向下。
am=(M+m)g/m,方向向下。
②当A运动到平衡位置下方最大位移处时,A有向上的最大加速度am,木块对地面的压力最大,又对整体由牛顿第二定律得:N-(M+m)g= M×0+mam,
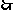 N=(M+m)g +mam=2(M+m)g,
N=(M+m)g +mam=2(M+m)g,
由牛顿第三定律得,B对地面的最大压力:
Nˊ=2(M+m)g,方向竖直向下。
③不加外力时,对m:kx0=mg
加外力F静止时,对m:k(x+x0)=F+mg
M刚离地面时对M:k(x-x0)=Mg
解以上方程得:F=(M+m)g.
21.解:振针的振动周期为T=0.2s,OA、AB等之间时间间隔为T,=T/2=0.1s,
又ΔS=AB-OA=2×10-2=aT,2,a=2m/s2。
由牛顿第二定律:F-mg=ma
得:F=m(g+a)=24(N)
20.解:由题意知T1=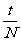 ,T2=
,T2=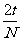 ,从而T1=T2/2。
,从而T1=T2/2。
又T1=2π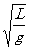 ,T2=2π
,T2=2π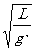
mg=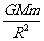 ,mg,=
,mg,=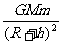
从而有:h=R=6.4×106(m)
19.解析:(1)设振幅为A,由题意BC=2A=10 cm,所以A=10 cm.振子从B到C所用时间t=0.5s.为周期T的一半,所以T=1.0s;f=1/T=1.0Hz.
(2)振子在1个周期内通过的路程为4A。故在t=5s=5T内通过的路程s=t/T×4A=200cm.5 s内振子振动了5个周期,5s末振子仍处在B点,所以它偏离平衡位置的位移大小为10cm.
(3)振子加速度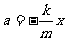 .a∝x,所以aB:aP=xB:xp=10:4=5:2.
.a∝x,所以aB:aP=xB:xp=10:4=5:2.
18.解析:如图所示,设振子的平衡位置为O,向下方向为正方向,此时弹簧的形变为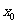 ,根据胡克定律及平衡条件有
,根据胡克定律及平衡条件有
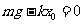 ①
①
当振子向下偏离平衡位置为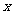 时,回复力(即合外力)为
时,回复力(即合外力)为
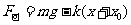 ②
②
将①代人②得: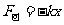 ,可见,重物振动时的受力符合简谐运动的条件.
,可见,重物振动时的受力符合简谐运动的条件.
点评:(1)分析一个振动是否为简谐运动,关键是判断它的回复力是否满足其大小与位移成正比,方向总与位移方向相反.证明思路为:确定物体静止时的位置--即为平衡位置,考查振动物体在任一点受到回复力的特点是否满足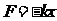 。(2)还要知道
。(2)还要知道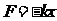 中的k是个比例系数,是由振动系统本身决定的,不仅仅是指弹簧的劲度系数.关于这点,在这里应理解为是简谐运动回复力的定义式.而且产生简谐运动的回复力可以是一个力,也可以是某个力的分力或几个力的合力.此题中的回复力为弹力和重力的合力.
中的k是个比例系数,是由振动系统本身决定的,不仅仅是指弹簧的劲度系数.关于这点,在这里应理解为是简谐运动回复力的定义式.而且产生简谐运动的回复力可以是一个力,也可以是某个力的分力或几个力的合力.此题中的回复力为弹力和重力的合力.
17.(1)步骤A中细线的上端应固定在悬点上(或用铁夹固定);
步骤C中应将单摆拉开一个很小的角度(例如不超过10°);
步骤F中应将每次实验的L 和T代入表达式分别求出g值,再取g的平均值;
(2)答案:①将钩码向下拉离平衡位置释放并测出N次全振动的时间t.
②由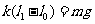 解得
解得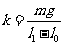 ,代入
,代入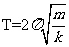 得出
得出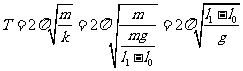
从而得出g=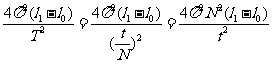
1.C 2.B 3.D 4.AD 5.AB 6.D 7.BC 8. AD 9. B 10.D 11.B 12.B 13.B 14.C 15.C 16. AD
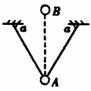
26.如图所示,用两根长度都为L的细绳悬挂一个小球A,绳 与水平方向的夹角为a .使球A垂直于纸面做摆角小于5°的摆动,当 它经过平衡位置的瞬间,另一小球B从A球的正上方自由下落,若B球 恰能击中A球,求B球下落的高度.
机械振动单元测试答案
25.在光滑的水平面上有一弹簧振子,弹簧的轻度系数为k,振子质量为M,振子的最大速度为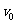 ,如图所示,当振子运动到最大位移为A的时刻把质量为m的物体轻放其上,求:
,如图所示,当振子运动到最大位移为A的时刻把质量为m的物体轻放其上,求:
(1)要保持物体和振子一起振动,二者间动摩擦因数至少 为多大?
(2)一起振动时,二者过平衡位置的速度多大?振幅又是多大?
24.如图所示,小球m自A点以向AD的方向的初速度V逐渐接近D点的小孔,已知AB弧长为0.8m,AB圆弧半径为R,AD=s,A、B、C、D位于同一水平面上,则V为多大时,才能使m恰好进入D处的小孔?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com