
7. 文学常识填空。(3分)
①《 》是我国第一部纪传体通史,课文《陈涉世家》即选自此书。
②《湖心亭看雪》是我国明末清初的文学家 的山水游记。
③《绿色蝈蝈》是 国的昆虫学家法布尔的作品。
6.补写出下列名句的上句或下句。(只选做3小题)(3分)
① ,各领风骚数百年。(赵翼《论诗》)
② 不畏浮云遮望眼, 。(王安石《登飞来峰》)
③ ,西出阳关无故人。(王维《送元二使安西》)
④先帝不以臣卑鄙,猥自枉屈, 。(诸葛亮《出师表》)
5.下列句子中标点符号使用不正确的一项是( )(3分)
A. 人生价值何在?人生出路又何在?他们面临着巨大的痛苦与困惑。
B. 凭着崇高的理想、豪迈的气概、乐观的志趣,克服困难不也是一种享受吗?
C. 黎明,葵花翘首向东迎日;正午,花盘追日转向南方;傍晚,花儿面西作别夕阳。
D. “管锥”二字出自《庄子·秋水》“用管窥天,用锥指地”,这为大家熟知。钱钟书用《管锥》命名自己的著作,谦逊之外则有深意,带有反讽的意味。
4. 填入下面横线上的语句,与上下文衔接最恰当的一项是( )(3分)
我们的时代,是百花齐放的时代,我们不但要盈亩满畦的牡丹和菊花,我们也要树下的紫罗兰,草地边的蒲公英。____我们的责任是不但让读者能兼收并蓄,而且还可以各取所需。
A. 世界上没有不爱花卉的人,但是每人的爱好又是多种多样的。
B. 世界上没有不爱花卉的人,但是每人的爱好不尽相同。
C. 因为每种花都有生存的权力,人们既爱牡丹.菊花,又爱紫罗兰.蒲公英。
D. 因为每种花都有生存的权力,那么每位读者也有选择的权力。
3.依次填入下列句子横线处的词语,最恰当的一项是( )(3分)
①秘书处听取并____了各位代表的提案,拟将其分类后,呈交主席团。
②程老领衔____ 《敦煌彩绘源流新证》,填补了敦煌艺术研究的空白。
③我正在欣赏着这里的景致,一位穿长袍戴小帽的老先生骑着一头小毛驴 ____走过我的身旁。
A. 搜集 编著 悠然自得 B.搜集 编纂 泰然自若
C. 收集 编纂 悠然自得 D.收集 编著 泰然自若
1..下列加点字的注音全都正确的一项是( )(3分)
A.嗜好(shì) 破绽 (dìng) 迸流 (bèng) 味同嚼蜡 (jiáo)
B.惬意 (xiá) 澎湃 (pài) 赫然 (hè) 泰然处之 (chǔ)
C.绮丽 (qǐ) 贮藏 (zhù) 枢纽 (qū) 茅塞顿开 (sè)
D.肇事 (zhào) 阻遏 (è) 荡涤 (dí) 鲜为人道 (xiǎn) 2.下列词语中没有错别字的一组是( )(3分)
A. 饶恕 不屈不挠 瑕疵 闻名遐迩 B. 渡假 渡过难关 范畴 一筹莫展
C. 涣散 沧海桑田 诀择 深恶痛绝 D. 契约 锲而不舍 青翠 山青水秀
数学教材是学习数学基础知识、形成基本技能的“蓝本”,能力是在知识传授和学习过程中得到培养和发展的。新课程试卷中平面向量的有些问题与课本的例习题相同或相似,虽然只是个别小题,但它对学习具有指导意义,教学中重视教材的使用应有不可估量的作用。因此,学习阶段要在掌握教材的基础上把各个局部知识按照一定的观点和方法组织成整体,形成知识体系。
学习本章主要树立数形转化和结合的观点,以数代形,以形观数,用代数的运算处理几何问题,特别是处理向量的相关位置关系,正确运用共线向量和平面向量的基本定理,计算向量的模、两点的距离等。由于向量是一新的工具,它往往会与三角函数、数列、不等式、解几等结合起来进行综合考查,是知识的交汇点.
(1)向量的加法与减法是互逆运算;
(2)相等向量与平行向量有区别,向量平行是向量相等的必要条件;
(3)向量平行与直线平行有区别,直线平行不包括共线(即重合),而向量平行则包括共线(重合)的情况;
(4)向量的坐标与表示该向量的有向线条的始点、终点的具体位置无关,只与其相对位置有关系.
题型1:平面向量的概念
例1.(1)给出下列命题:
①若| |=|
|=| |,则
|,则 =
= ;
;
②若A,B,C,D是不共线的四点,则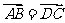 是四边形ABCD为平行四边形的充要条件;
是四边形ABCD为平行四边形的充要条件;
③若 =
= ,
, =
=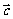 ,则
,则 =
=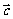 ;
;
④ =
= 的充要条件是|
的充要条件是| |=|
|=| |且
|且 //
// ;
;
⑤ 若 //
// ,
, //
//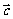 ,则
,则 //
//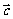 ;
;
其中正确的序号是
。
(2)设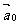 为单位向量,(1)若
为单位向量,(1)若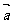 为平面内的某个向量,则
为平面内的某个向量,则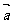 =|
=|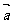 |·
|·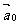 ;(2)若
;(2)若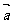 与a0平行,则
与a0平行,则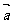 =|
=|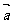 |·
|·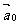 ;(3)若
;(3)若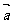 与
与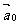 平行且|
平行且|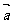 |=1,则
|=1,则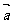 =
=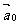 。上述命题中,假命题个数是( )
。上述命题中,假命题个数是( )
A.0 B.1 C.2 D.3
解析:(1)①不正确.两个向量的长度相等,但它们的方向不一定相同;
②正确;∵ 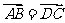 ,∴
,∴ 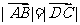 且
且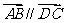 ,
,
又 A,B,C,D是不共线的四点,∴ 四边形 ABCD为平行四边形;反之,若四边形ABCD为平行四边形,则,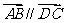 且
且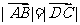 ,
,
因此,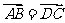 。
。
③正确;∵  =
= ,∴
,∴  ,
, 的长度相等且方向相同;
的长度相等且方向相同;
又 =
=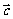 ,∴
,∴  ,
,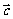 的长度相等且方向相同,
的长度相等且方向相同,
∴  ,
,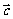 的长度相等且方向相同,故
的长度相等且方向相同,故 =
=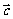 。
。
④不正确;当 //
// 且方向相反时,即使|
且方向相反时,即使| |=|
|=| |,也不能得到
|,也不能得到 =
= ,故|
,故| |=|
|=| |且
|且 //
// 不是
不是 =
= 的充要条件,而是必要不充分条件;
的充要条件,而是必要不充分条件;
⑤不正确;考虑 =
=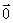 这种特殊情况;
这种特殊情况;
综上所述,正确命题的序号是②③。
点评:本例主要复习向量的基本概念。向量的基本概念较多,因而容易遗忘。为此,复习时一方面要构建良好的知识结构,另一方面要善于与物理中、生活中的模型进行类比和联想。
(2)向量是既有大小又有方向的量,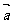 与|
与|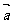 |
|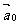 模相同,但方向不一定相同,故(1)是假命题;若
模相同,但方向不一定相同,故(1)是假命题;若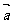 与
与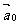 平行,则
平行,则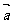 与
与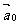 方向有两种情况:一是同向二是反向,反向时
方向有两种情况:一是同向二是反向,反向时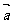 =-|
=-|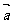 |
|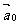 ,故(2)、(3)也是假命题。综上所述,答案选D。
,故(2)、(3)也是假命题。综上所述,答案选D。
点评:向量的概念较多,且容易混淆,故在学习中要分清,理解各概念的实质,注意区分共线向量、平行向量、同向向量等概念。
题型2:平面向量的运算法则
例2.(1)如图所示,已知正六边形ABCDEF,O是它的中心,若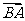 =
= ,
,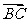 =
= ,试用
,试用 ,
, 将向量
将向量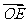 ,
,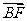 ,
,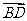 ,
, 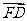 表示出来。
表示出来。
(1)解析:根据向量加法的平行四边形法则和减法的三角形法则,用向量 ,
, 来表示其他向量,只要考虑它们是哪些平行四边形或三角形的边即可。
来表示其他向量,只要考虑它们是哪些平行四边形或三角形的边即可。
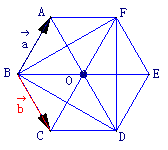 因为六边形ABCDEF是正六边形,所以它的中心O及顶点A,B,C四点构成平行四边形ABCO,
因为六边形ABCDEF是正六边形,所以它的中心O及顶点A,B,C四点构成平行四边形ABCO,
所以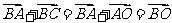 ,
, =
= +
+ ,
,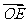 =
=  =
= +
+ ,
,
由于A,B,O,F四点也构成平行四边形ABOF,所以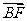 =
= +
+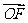 =
= +
+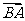 =
= +
+ +
+ =2
=2 +
+ ,
,
同样在平行四边形 BCDO中,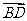 =
= =
=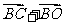 =
= +(
+( +
+ )=
)= +2
+2 ,
,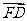 =
=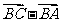 =
= -
- 。
。
点评:其实在以A,B,C,D,E,F及O七点中,任两点为起点和终点,均可用
 ,
, 表示,且可用规定其中任两个向量为
表示,且可用规定其中任两个向量为 ,
, ,另外任取两点为起点和终点,也可用
,另外任取两点为起点和终点,也可用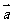 ,
, 表示。
表示。
 (3)(2008湖南文,4)
(3)(2008湖南文,4)
11.已知向量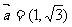 ,
,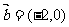 ,则
,则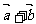 =_____________________.
=_____________________.
[答案]2
[解析]由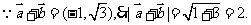
(4)(2009年广东卷文)已知平面向量a= ,b=
,b= , 则向量
, 则向量 ( )
( )
A平行于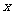 轴 B.平行于第一、三象限的角平分线
轴 B.平行于第一、三象限的角平分线
C.平行于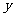 轴 D.平行于第二、四象限的角平分线
轴 D.平行于第二、四象限的角平分线
答案 C
解析 
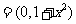 ,由
,由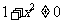 及向量的性质可知,C正确.
及向量的性质可知,C正确.
例4.设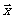 为未知向量,
为未知向量, 、
、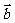 为已知向量,解方程2
为已知向量,解方程2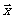 -(5
-(5 +3
+3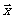 -4
-4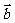 )+
)+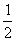
 -3
-3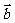 =0.
=0.
解析:原方程可化为:(2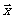 - 3
- 3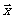 ) + (-5
) + (-5 +
+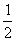
 ) + (4
) + (4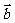 -3
-3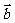 ) = 0,
) = 0,
∴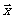 =
=
 +
+ 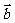 。
。
点评:平面向量的数乘运算类似于代数中实数与未知数的运算法则,求解时兼顾到向量的性质。
题型3:平面向量的坐标及运算
例5.已知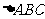 中,A(2,-1),B(3,2),C(-3,1),BC边上的高为AD,求
中,A(2,-1),B(3,2),C(-3,1),BC边上的高为AD,求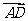 。
。
解析:设D(x,y),则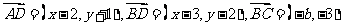
∵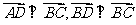
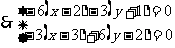 得
得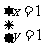
所以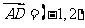 。
。
例6.已知点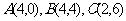 ,试用向量方法求直线
,试用向量方法求直线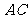 和
和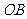 (
(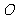 为坐标原点)交点
为坐标原点)交点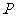 的坐标。
的坐标。
解析:设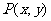 ,则
,则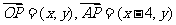
因为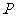 是
是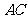 与
与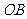 的交点,所以
的交点,所以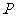 在直线
在直线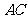 上,也在直线
上,也在直线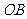 上。
上。
即得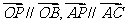 ,由点
,由点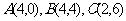 得,
得,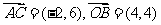 。
。
得方程组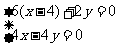 ,解之得
,解之得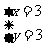 。
。
故直线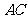 与
与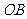 的交点
的交点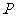 的坐标为
的坐标为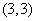 。
。
题型4:平面向量的性质
例7.平面内给定三个向量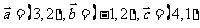 ,回答下列问题:
,回答下列问题:
(1)求满足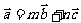 的实数m,n;
的实数m,n;
(2)若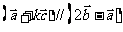 ,求实数k;
,求实数k;
(3)若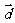 满足
满足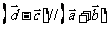 ,且
,且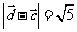 ,求
,求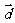 。
。
解析:(1)由题意得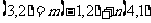 ,所以
,所以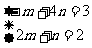 ,得
,得 。
。
(2)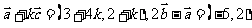 ,
,
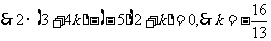 ;
;
(3)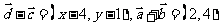
由题意得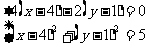 ,得
,得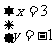 或
或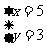 。
。
例8.已知
(1)求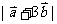 ;
;
(2)当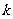 为何实数时,
为何实数时,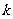

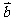 与
与 平行, 平行时它们是同向还是反向?
平行, 平行时它们是同向还是反向?
解析:(1)因为
所以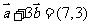
则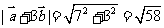
(2)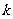

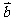
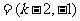 ,
,
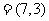
因为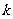

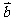 与
与 平行,所以
平行,所以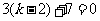 即得
即得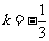 。
。
此时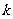

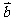
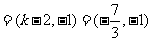 ,
,
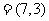 ,则
,则
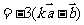 ,即此时向量
,即此时向量 与
与 方向相反。
方向相反。
点评:上面两个例子重点解析了平面向量的性质在坐标运算中的体现,重点掌握平面向量的共线的判定以及平面向量模的计算方法。
题型5:共线向量定理及平面向量基本定理
例9.(2009北京卷文)已知向量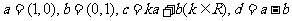 ,如果
,如果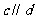
那么 ( )
A.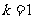 且
且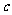 与
与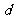 同向
B.
同向
B.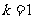 且
且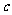 与
与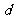 反向
反向
C.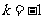 且
且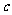 与
与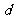 同向
D.
同向
D.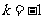 且
且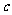 与
与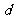 反向
反向
答案 D
解析 本题主要考查向量的共线(平行)、向量的加减法. 属于基础知识、基本运算考查.
∵a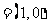 ,b
,b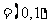 ,若
,若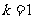 ,则c
,则c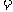 a
a b
b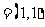 ,d
,d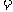 a
a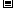 b
b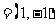 ,
,
显然,a与b不平行,排除A、B.
若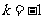 ,则c
,则c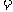
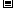 a
a b
b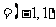 ,d
,d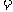
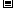 a
a b
b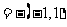 ,
,
即c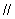 d且c与d反向,排除C,故选D.
d且c与d反向,排除C,故选D.
点评:熟练运用向量的加法、减法、实数与向量的积的坐标运算法则进行运算;两个向量平行的坐标表示;运用向量的坐标表示,使向量的运算完全代数化,将数与形有机的结合。
例10.(1)(06福建理,11)已知︱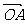 ︱=1,︱
︱=1,︱ ︱=
︱=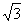 ,
,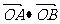 =0,点C在∠AOB内,且∠AOC=30°,设
=0,点C在∠AOB内,且∠AOC=30°,设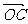 =m
=m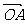 +n
+n (m、n∈R),则
(m、n∈R),则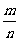 等于( )
等于( )
A.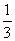 B.3
C.
B.3
C.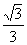 D.
D.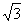
(2)(2009安徽卷理)给定两个长度为1的平面向量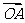 和
和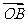 ,它们的夹角为
,它们的夹角为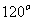 .
.
 如图所示,点C在以O为圆心的圆弧
如图所示,点C在以O为圆心的圆弧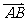 上变动.
上变动.
若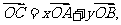 其中
其中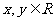 ,则
,则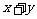
的最大值是________.
答案 2
解析 设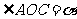
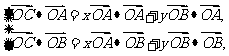 ,即
,即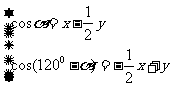
∴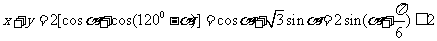
题型6:平面向量综合问题
例11.(2009上海卷文) 已知ΔABC的角A、B、C所对的边分别是a、b、c,设向量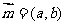 ,
,
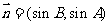 ,
, .
.
(1)
若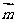 //
//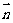 ,求证:ΔABC为等腰三角形;
,求证:ΔABC为等腰三角形;
(2)
若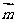 ⊥
⊥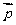 ,边长c = 2,角C =
,边长c = 2,角C = 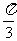 ,求ΔABC的面积 .
,求ΔABC的面积 .
证明:(1)
即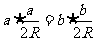 ,其中R是三角形ABC外接圆半径,
,其中R是三角形ABC外接圆半径,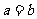
 为等腰三角形
为等腰三角形
解(2)由题意可知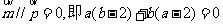
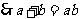
由余弦定理可知,
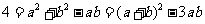


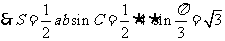
5.平面向量的坐标表示
(1)平面向量的坐标表示:在直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量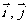 作为基底.由平面向量的基本定理知,该平面内的任一向量
作为基底.由平面向量的基本定理知,该平面内的任一向量 可表示成
可表示成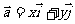 ,由于
,由于 与数对(x,y)是一一对应的,因此把(x,y)叫做向量
与数对(x,y)是一一对应的,因此把(x,y)叫做向量 的坐标,记作
的坐标,记作 =(x,y),其中x叫作
=(x,y),其中x叫作 在x轴上的坐标,y叫做在y轴上的坐标。
在x轴上的坐标,y叫做在y轴上的坐标。
规定:
(1)相等的向量坐标相同,坐标相同的向量是相等的向量;
(2)向量的坐标与表示该向量的有向线段的始点、终点的具体位置无关,只与其相对位置有关系。
(2)平面向量的坐标运算:
①若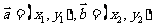 ,则
,则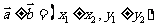 ;
;
②若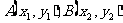 ,则
,则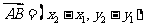 ;
;
③若 =(x,y),则
=(x,y),则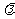
 =(
=(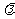 x,
x, 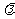 y);
y);
④若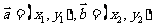 ,则
,则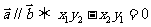 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com