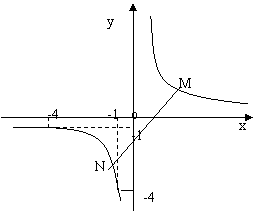
9.(2008年乐山市)题乙：图(14)是反比例函数的图象，当－4≤x≤－1时，－4≤y≤－1

(1)　　　 求该反比例函数的解析式

(2)　　　 若M、N分别在反比例函数图象的两支上，请指出什么情况下线段MN最短(不需证明)，并求出线段MN长度的取值范围

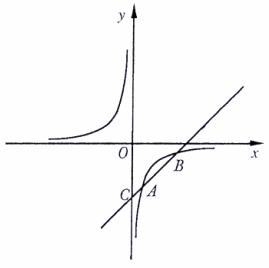
8.(2008年成都市)如图，已知反比例函数y = 的图象经过点A(1，- 3)，一次函数y = kx + b的图象经过点A与点C(0，- 4)，且与反比例函数的图象相交于另一点B.

(1)试确定这两个函数的表达式；

(2)求点B的坐标.

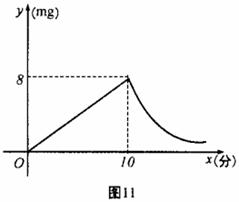
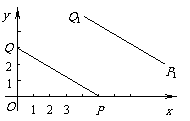
7.(2008年四川巴中市)为预防“手足口病”，某校对教室进行“药熏消毒”．已知药物燃烧阶段，室内每立方米空气中的含药量(mg)与燃烧时间(分钟)成正比例；燃烧后，与成反比例(如图所示)．现测得药物10分钟燃完，此时教室内每立方米空气含药量为8mg．据以上信息解答下列问题：

(1)求药物燃烧时与的函数关系式．

(2)求药物燃烧后与的函数关系式．

(3)当每立方米空气中含药量低于1.6mg时，对人体方能无毒害作用，那么从消毒开始，经多长时间学生才可以回教室？

6.(2008年天津市)已知点P(2，2)在反比例函数()的图象上，

(Ⅰ)当时，求的值；

(Ⅱ)当时，求的取值范围．

5. (2008年山东省滨州市)(1)探究新知：

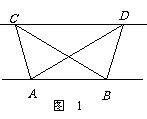
如图1，已知△ABC与△ABD的面积相等，试判断AB与CD的位置关系，并说明理由.

(2)结论应用：

①如图2，点M、N在反比例函数y=的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F.

试应用(1)中得到的结论证明：MN∥EF.

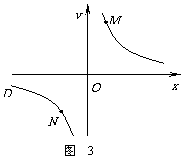
②若①中的其他条件不变，只改变点M，N的位置如图3所示，

请判断MN与E是否平行.

4．(2008山东威海)如图，点A(m，m+1)，B(m+3，m－1)都在反比例函数的图象上．　　

(1)求m，k的值；　

(2)如果M为x轴上一点，N为y轴上一点，

以点A，B，M，N为顶点的四边形是平行四边形，　

试求直线MN的函数表达式．　 　

(3)选做题：在平面直角坐标系中，点P的坐标

为(5，0)，点Q的坐标为(0，3)，把线段PQ向右平

移4个单位，然后再向上平移2个单位，得到线段P₁Q₁，

则点P₁的坐标为　　　　 ，点Q₁的坐标为　　　 ．

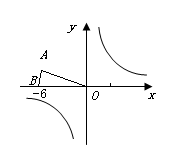
3.(2008浙江义乌)已知：等腰三角形OAB在直角坐标系中的位置如图，点A的坐标为()，点B的坐标为(－6，0).

(1)若三角形OAB关于y轴的轴对称图形是三角形O，

请直接写出A、B的对称点的坐标；

(2)若将三角形沿x轴向右平移a个单位，此时点A

恰好落在反比例函数的图像上，求a的值；

(3)若三角形绕点O按逆时针方向旋转度().

①当=时点B恰好落在反比例函数的图像上，求k的值．

②问点A、B能否同时落在①中的反比例函数的图像上，若能，求出

的值；若不能，请说明理由.

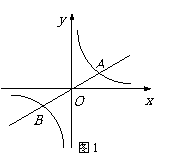
2. (2008淅江金华)如图1，已知双曲线y=(k>0)与直线y=k′x交于A，B两点，点A在第一象限.试解答下列问题：(1)若点A的坐标为(4，2).则点B的坐标为　　　 ；若点A的横坐标为m，则点B的坐标可表示为　　　 ；

(2)如图2，过原点O作另一条直线l，交双曲线y=(k>0)于P，Q两点，点P在第一象限.①说明四边形APBQ一定是平行四边形；②设点A.P的横坐标分别为m，n，四边形APBQ可能是矩形吗?可能是正方形吗?若可能，直接写出mn应满足的条件；若不可能，请说明理由.

1. (08山东省日照市)(1)探究新知：

如图1，已知△ABC与△ABD的面积相等，

试判断AB与CD的位置关系，并说明理由．

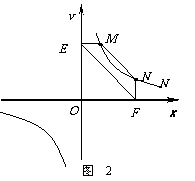
(2)结论应用：　

① 如图2，点M，N在反比例函数(k＞0)的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F．

试证明：MN∥EF．　

② 若①中的其他条件不变，只改变点M，N

的位置如图3所示，请判断 MN与EF是否平行．

24.(2008年四川省宜宾市)若正方形AOBC的边OA、OB在坐标轴上，顶点C在第一象限且在反比例函数y=的图像上，则点C的坐标是