[例1]求角(用反三角函数表示):

(1)已知tanx=3,x∈[0.2π]求x的值;

(2)已知cos2α=,α∈(0,),sinβ=-,β∈(π, 　)

求α+β.

解：(1)在上,时,tanx=3;

在上,,

∴x=arctan3或π+arctan3.

(2)由;得

sinα=,从而cosα=,且cosβ=-

又α+β∈(π,2π)?

cos(α+β)=cosαcosβ-sinαsinβ=-.

∴α+βπ=

即α+β=2π-arccos

◆提炼方法：求角先求三角函数值,求什么三角函数值要先看角的范围,如本题(2)应求余弦而不能求正弦.角不在主值区间时,要借助图象、三角函数线或诱导公式写出符合条件的角。

[例2](2007启东质检)已知A、B、C是三内角，向量，且，

(1)求角A；

(2)若，求

解:(1)∵ ∴，即

,

∵，∴，∴

(2)由题知，整理得

∴，∴，∴或

而使，舍去，∴

∴

[例3]在某海滨城市附近海面有一台风，据检测，当前台

风中心位于城市O(如图)的东偏南方向

300 km的海面P处，并以20 km / h的速度向西偏北的

方向移动，台风侵袭的范围为圆形区域，当前半径为60 km ，

并以10 km / h的速度不断增加，问几小时后该城市开始受到

台风的侵袭。

解法一:设在时刻t(h)台风中心为Q,此时台风侵袭的圆形区域半径为10t+60(km)

若在时刻t城市O受到台风的侵袭,则

由余弦定理知

由于PO=300,PQ=20t

故

因此

解得

解法二:如图建立坐标系：以O为原点，正东方向为x轴正向. 在时刻：t(h)台风中心的坐标为

　 此时台风侵袭的区域是，其中t+60，

　 若在t时，该城市O受到台风的侵袭，则有

即

即，　 解得.

答：12小时后该城市开始受到台风气侵袭

◆提炼方法：实际应用问题，要从中找出题中的三角形和已知的边角等条件，再设计出合理的解题方案。

[例4]已知函数的图象向右平移个单位得到函数的图象.　 ⑴求函数的表达式;

⑵证明当时，经过函数图象上任意两点的直线的斜率恒大于零.

解：(I)

(II)证明一：依题意，只需证明函数g(x)当时是增函数

在即的每一个区间上是增函数

当时，在是增函数,则当时，经过函数g(x)图像上任意两点的直线的斜率恒大于零

[研讨.欣赏]某城市有一条公路，自西向东经过A点到市中心O点后转向东北方向OB，现要修建一条铁路L，L在OA上设一站A，在OB上设一站B，铁路在AB部分为直线段，现要求市中心O与AB的距离为10 km，问把A、B分别设在公路上离中心O多远处才能使|AB|最短?并求其最短距离.(不要求作近似计算)

解：在△AOB中，设OA=a，OB=b.

因为AO为正西方向，OB为东北方向，所以∠AOB=135°.

又O到AB的距离为10.

∴

设∠OAB=α，则∠OBA=45°－α.

所以a=，b=，

ab=·

=

=

=≥，

当且仅当α=22°30′ 时，“=”成立.

所以|AB|²≥=400(+1)²，

当且仅当a=b，α=22°30′时，“=”成立.

所以当a=b==10时，即当AB分别在OA、OB上离O点10 km处，能使|AB|最短，最短距离为20(－1).

法二;

…

法三:|AB|²=a²+b²－2abcos135°=a²+b²+ab≥2ab+ab=(2+)ab，…

◆温馨提示:1.若直接建立|AB|²与角α的函数关系,求最值值困难;

2.先视|AB|²为a,b的函数放缩,再把ab看成α的函数求出最小值;

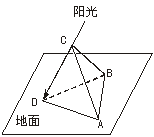
4.作CE⊥平面ABD于E，则∠CDE=40°,延长DE交直线AB于F，则∠CFD是遮阳棚与地面所成的角，在△CFD中，=.∴DF=.当α=50°时，DF最大.答案：C;　 5.; 6. 最大值为1+=.

3.sinA₂=cosA₁,……A₁、B₁、C₁是锐角。如果A₂、B₂、C₂也是锐角，则，矛盾，故选D。

6．(2004北京西城二模)函数y=sinx(sinx+cosx)(x∈R)的最大值是_______.

◆答案:1-4.CBDC; 2.A+B＞.∴A＞－B，B＞－A.

∴sinA＞cosB，sinB＞cosA.,P在第二象限.

5．(2003上海)若x=是方程2cos(x+α)=1的解，其中α∈(0，2π)，则α=_________.

4. 如图，△ABC是简易遮阳棚，A、B是南北方向上两个定点，正东方向射出的太阳光线与地面成40°角，为了使遮阴影面ABD面积最大，遮阳棚ABC与地面所成的角为

A.75°　　　　　　　　　 B.60°　　　　　 C.50°　　　　　 D.45°

3．的三个内角的余弦值分别等于的三个内角的正弦值，则(　 )

A．和都是锐角三角形

B．和都是钝角三角形

C．是钝角三角形，是锐角三角形

D．是锐角三角形，是钝角三角形

2.若A、B是锐角△ABC的两个内角，则点P(cosB－sinA，sinB－cosA)在(　 )

A.第一象限　　 B.第二象限　 C.第三象限　 D.第四象限

1. 已知，则x等于　 (　 )

4．在应用与综合性题目中,当角不是特殊角,要“用反三角函数表示角”:

(1)

(2)arccosa表示[0，π]上余弦值等于a的角,a∈[－1,1];

(3)

(4) 对于不是上述范围内的角,可借助诱导公式和三角函数线,找出与上述反三角的关系进而求出. 例如:sinα=0.3, α是钝角,则α=π－arcsin0.3.