
2.作为实义动词时, 可用于: dare to do sth
a. Little Jane didn’t dare to go alone.
b. Did you dare to go out alone at night ?
第十章:虚拟语气
概 述
1.作为情态动词时, 主要用于否定句和疑问句中, 不用于肯定句中
a. Little Jane dared not go alone. =Little Jane didn’t dare to go alone.
b. Dare you go out alone at night ? =Did you dare to go out alone at night ?
3.对于用need的提问, 肯定回答用must, 否定回答用needn’t
a. Need I come? Yes, you must. / No, you needn’t.
2.need作情态动词时, 多用于否定句及疑问句中, 不用于肯定句中
a. It is still early. You needn’t hurry. =You don’t need to hurry.
b. It is 11 o’clock. Need I go now? =Do I need to go now ?
1.need作实义动词时, 注意以下用法:
①.need to do sth; ②.need sb to do sth; ③.need doing sth (主动形式表被动意义)
a. You need to remain in bed.
b. I need you to help me with the housework.
c. The garden needs watering.( =The garden needs to be watered.)
10. 中,内角
中,内角 .
. .
. 的对边分别为
的对边分别为 .
. .
. ,已知
,已知 .
. .
. 成等比数列,且
成等比数列,且

(1)求 的值;
的值;
(2)若 ,求
,求 的值
的值
解:(1)由
 得:
得:
由 及正弦定理得:
及正弦定理得:
于是:

(2)由 得:
得: ,因
,因
 ,所以:
,所以: ,即:
,即:
由余弦定理 得:
得:
于是:
故:a+c
[探索题](2005上海)对定义域是 .
. 的函数
的函数 .
. ,
,
规定:函数
(1)若函数 ,
, ,写出函数
,写出函数 的解析式;
的解析式;
(2)求问题(1)中函数 的值域;
的值域;
(3)若 ,其中
,其中 是常数,且
是常数,且 ,请设计一个定义域为R的函数
,请设计一个定义域为R的函数 ,及一个
,及一个 的值,使得
的值,使得 ,并予以证明
,并予以证明
[解] (1)
(2) 当x≠1时, h(x)=  =x-1+
=x-1+ +2,
+2,
若x>1时, 则h(x)≥4,其中等号当x=2时成立
若x<1时, 则h(x)≤ 0,其中等号当x=0时成立
∴函数h(x)的值域是(-∞,0]∪{1}∪[4,+∞)
(3)令 f(x)=sin2x+cos2x,α=
则g(x)=f(x+α)= sin2(x+ )+cos2(x+
)+cos2(x+ )=cos2x-sin2x,
)=cos2x-sin2x,
于是h(x)= f(x)·f(x+α)= (sin2x+co2sx)( cos2x-sin2x)=cos4x.
另解令f(x)=1+ sin2x, α=
sin2x, α= ,
,
g(x)=f(x+α)=
1+ sin2(x+π)=1-
sin2(x+π)=1- sin2x,
sin2x,
于是h(x)= f(x)·f(x+α)= (1+ sin2x)( 1-
sin2x)( 1- sin2x)=cos4x.
sin2x)=cos4x.
9. P是以F1、F2为焦点的椭圆上一点,且∠PF1F2=α,∠PF2F1=2α,求证:椭圆的离心率为e=2cosα-1.
剖析:依据椭圆的定义2a=|PF1|+|PF2|,2c=|F1F2|,
 ∴e=
∴e= .
.
在△PF1F2中解此三角即可得证.
证明:在△PF1F2中,由正弦定理知
 =
= =
= .
.
由比例的性质得 =
=
 e=
e= =
= =
=
=
= =2cosα-1.
=2cosα-1.
评述:恰当地利用比例的性质有事半功倍之效.
8.为进行科学实验,观测小球A、B在两条相交成 角的直线型轨道上运动的情况,如图所示,运动开始前,A和B分别距O点3m和1m,后来它们同时以每分钟4m的速度各沿轨道
角的直线型轨道上运动的情况,如图所示,运动开始前,A和B分别距O点3m和1m,后来它们同时以每分钟4m的速度各沿轨道 按箭头的方向运动。问:
按箭头的方向运动。问:
(I)运动开始前,A、B的距离是多少米?(结果保留三位有效数字)。
(Ⅱ)几分钟后,两个小球的距离最小?
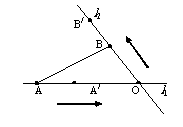

解:小球开始运动前的距离为:

(2)设t分钟后,小球A、B分别运动到A’、B’处,则
当 时,
时,

当 时,
时,

故


 当
当 ,
,
故 分钟后两个小球的距离最小。
分钟后两个小球的距离最小。
7.(1)已知 ,求角
,求角 的集合;
的集合;
(2)已知cosx=-0.4,x∈[0,2π],求角x的集合.
解:先找出一个周期上的角,再加上周期.
(1) 在 上,
上, ;
; 
在 上,
上, ,
,
所求角x的集合为:
(常写成 )
)
(2) 当 ;
;
当
综上得
5. ; 6. y=
; 6. y= .令
.令 =m,m∈(
=m,m∈( ,1),
,1),
则y=-2m2+3m-1.∈(0, ].
].
[解答题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com