
1.余弦定理:三角形任何一边的平方等于其他两边平方的和,减去这两边与它们夹角的余弦的积的2倍,即
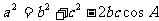
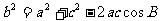
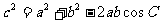
[例1] 和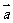 = (3,-4)平行的单位向量是_________;
= (3,-4)平行的单位向量是_________;

错解:因为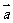 的模等于5,所以与
的模等于5,所以与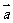 平行的单位向量就是
平行的单位向量就是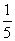
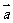 ,即 (,-)
,即 (,-)

错因:在求解平行向量时没有考虑到方向相反的情况。

正解:因为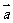 的模等于5,所以与
的模等于5,所以与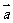 平行的单位向量是
平行的单位向量是
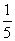
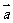 ,即(,-)或(-,)
,即(,-)或(-,)

点评:平行的情况有方向相同和方向相反两种。读者可以自己再求解“和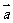 = (3,-4)垂直的单位向量”,结果也应该是两个。
= (3,-4)垂直的单位向量”,结果也应该是两个。

[例2]已知A(2,1),B(3,2),C(-1,4),若A、B、C是平行四边形的三个顶点,求第四个顶点D的坐标。

错解:设D的坐标为(x,y),则有x-2=-1-3,y-1=4-2 ,即x=-2,y=3。故所求D的坐标为(-2,3)。

错因:思维定势。习惯上,我们认为平行四边形的四个顶点是按照ABCD的顺序。其实,在这个题目中,根本就没有指出四边形ABCD。因此,还需要分类讨论。

正解:设D的坐标为(x,y)

当四边形为平行四边形ABCD时,有x-2=-1-3,y-1= 4-2 ,即x=
-2,y= 3。解得D的坐标为(-2,3);

当四边形为平行四边形ADBC时,有x-2=3-(-1),y-1= 2-4 ,即x= 6,y= -1。解得D的坐标为(6,-1);

当四边形为平行四边形ABDC时,有x-3=-1-2,y-2= 4-1 ,即x=
0,y= 5。解得D的坐标为(0,5)。

故第四个顶点D的坐标为(-2,3)或(6,-1)或(0,5)。

[例3]已知P1(3,2),P2(8,3),若点P在直线P1P2上,且满足|P1P|=2|PP2|,求点P的坐标。

错解:由|P1P|=2|PP2|得,点P 分P1P2所成的比为2,代入定比分点坐标公式得P(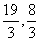 )
)

错因:对于|P1P|=2|PP2|这个等式,它所包含的不仅是点P为 P1,P2
的内分点这一种情况,还有点P是 P1,P2的外分点。故须分情况讨论。

正解:当点P为 P1,P2
的内分点时,P 分P1P2所成的比为2,此时解得P(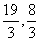 );
);

当点P为 P1,P2
的外分点时,P 分P1P2所成的比为-2,此时解得P(13,4)。

则所求点P的坐标为(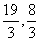 )或(13,4)。
)或(13,4)。

点评:在运用定比分点坐标公式时,要审清题意,注意内外分点的情况。也就是分类讨论的数学思想。

[例4] 设向量 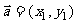 ,
,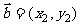 ,
, ,则“
,则“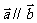 ”是“
”是“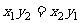 ”的
”的

A.充分不必要条件
B.必要不充分条件

C.充要条件
D.既不充分也不必要条件

分析:根据向量的坐标运算和充要条件的意义进行演算即可.

解:若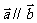 ,∵
,∵ ,则
,则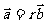 ,代入坐标得:
,代入坐标得: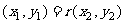 ,即
,即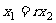 且
且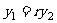 .消去
.消去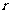 ,得
,得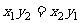 ;
;

反之,若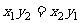 ,则
,则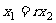 且
且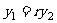 ,即
,即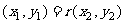


则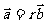 ,∴
,∴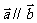


故“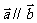 ”是“
”是“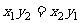 ”的充要条件.
”的充要条件.

答案:C

点评:本题意在巩固向量平行的坐标表示.

[例5].已知 =(1,-1),
=(1,-1), =(-1,3),
=(-1,3),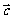 =(3,5),求实数x、y,使
=(3,5),求实数x、y,使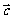 =x
=x +y
+y .
.

分析:根据向量坐标运算和待定系数法,用方程思想求解即可.

解:由题意有

x +y
+y =x(1,-1)+y(-1,3)=(x-y,-x+3y).
=x(1,-1)+y(-1,3)=(x-y,-x+3y).

又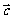 =(3,5)
=(3,5)

∴x-y=3且-x+3y=5

解之得 x=7 且y=4

点评:在向量的坐标运算中经常要用到解方程的方法.

[例6]已知A(-1,2),B(2,8),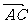 =
=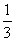
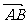 ,
,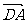 = -
= -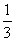
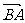 ,求点C、D和向量
,求点C、D和向量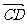 的坐标.
的坐标.

分析:待定系数法设定点C、D的坐标,再根据向量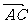
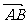 ,
,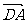 和
和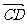 关系进行坐标运算,用方程思想解之.
关系进行坐标运算,用方程思想解之.

解:设C、D的坐标为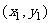 、
、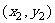 ,由题意得
,由题意得

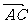 =(
=(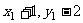 ),
),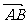 =(3,6),
=(3,6), 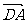 =(
=(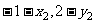 ),
),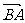 =(-3,-6)
=(-3,-6)

又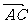 =
=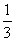
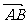 ,
,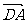 = -
= -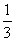
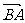


∴(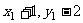 )=
)=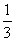 (3,6), (
(3,6), (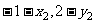 )=-
)=-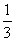 (-3,-6)
(-3,-6)
即 (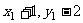 )=(1,2) , (
)=(1,2) , (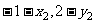 )=(1,2)
)=(1,2)
∴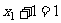 且
且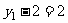 ,
,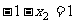 且
且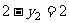
∴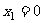 且
且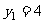 ,且
,且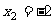
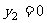
∴点C、D和向量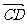 的坐标分别为(0,4)、(-2,0)和(-2,-4)
的坐标分别为(0,4)、(-2,0)和(-2,-4)
小结:本题涉及到方程思想,对学生运算能力要求较高.
§8.2平面向量与代数、几何的综合应用
5.平移公式中首先要知道这个公式是点的平移公式,故在使用的过程中须将起始点的坐标给出,同时注意顺序。

4.定比分点公式中则要记清哪个点是分点;还有就是此公式中横坐标和纵坐标是分开计算的;

3.对于坐标形式给出的两个向量,在运用平行与垂直的充要条件时,一定要区分好两个公式,切不可混淆。因此,建议在记忆时对比记忆;

2.在运用三角形法则和平行四边形法则求向量的加减法时要注意起点和终点;

1.向量的概念的理解,尤其是特殊向量“零向量”

向量是既有大小,又有方向的量.向量的模是正数或0,是可以进行大小比较的,由于方向不能比较大小,所以向量是不能比大小的.两个向量的模相等,方向相同,我们称这两个向量相等,两个零向量是相等的,零向量与任何向量平行,与任何向量都是共线向量;

12.平移公式:

设P(x,y)是图形F上的任意一点,它在平移后图形F/上对应点为P/(x/,y/),且设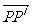 的坐标为(h,k),则由
的坐标为(h,k),则由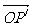 =
=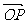 +
+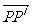 ,得:(x/,y/)=(x,y)+(h,k)
,得:(x/,y/)=(x,y)+(h,k)

11.平面向量的数量积

(1)定义:已知两个非零向量 和
和 ,它们的夹角为θ,则数量|
,它们的夹角为θ,则数量| ||
|| |cosθ叫做
|cosθ叫做 与
与 的数量积(或内积),记作
的数量积(或内积),记作 ·
· ,即
,即 ·
· =|
=| ||
|| |cosθ
|cosθ

规定:零向量与任一向量的数量积是0。

(2)几何意义:数量积 ·
· 等于
等于 的长度|
的长度| |与
|与 在
在 的方向上的投影|
的方向上的投影| |cosθ的乘积。
|cosθ的乘积。

(3)性质:设 ,
, 都是非零向量,
都是非零向量,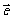 是与
是与 方向相同的单位向量,θ是
方向相同的单位向量,θ是 与
与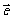 的夹角,则
的夹角,则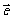 ·
· =
= ·
·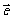 =|
=| |cosθ ,
|cosθ , ⊥
⊥
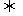
 ·
· =0
=0

当 与
与 同向时,
同向时, ·
· =|
=| ||
|| |
|

当 与
与 反向时,
反向时, ·
· =-|
=-| ||
|| |
|

特别地, ·
· =|
=| |2或|
|2或| |=
|=


cosθ= |
| ·
· |≤|
|≤| ||
|| |
|

(4)运算律:

 ·
· =
= ·
· (交换律)
(交换律)

(λ )·
)· =λ(
=λ( ·
· )=
)= ·(λ
·(λ )
)

( +
+ )·
)·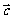 =
= ·
· +
+ ·
·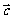


(5)平面向量垂直的坐标表示的充要条件:

设 =(x1 ,y1),
=(x1 ,y1),  = (x2,y2),则
= (x2,y2),则


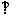

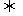
 ·
· =|
=| |·|
|·| |cos90°=0
|cos90°=0


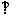

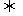 x1x2+y1y2=0
x1x2+y1y2=0

10.定比分点

设P1,P2是直线l上的两点,点P是不同于P1,P2的任意一点则存在一个实数λ,使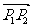 =λ
=λ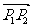 ,λ叫做分有向线段所成的比。若点P1、P、P2的坐标分别为(x1,y1),(x,y),(x2,y2),则有
,λ叫做分有向线段所成的比。若点P1、P、P2的坐标分别为(x1,y1),(x,y),(x2,y2),则有

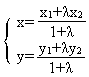


特别当λ=1,即当点P是线段P1P2的中点时,有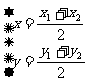


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com