
12.(2009安徽卷理)(本小题满分12分)
已知函数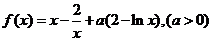 ,讨论
,讨论 的单调性.
的单调性.
本小题主要考查函数的定义域、利用导数等知识研究函数的单调性,考查分类讨论的思想方法和运算求解的能力。本小题满分12分。
解: 的定义域是(0,+
的定义域是(0,+ ),
), 21世纪教育网
21世纪教育网 

设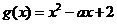 ,二次方程
,二次方程 的判别式
的判别式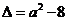 .
.
①
当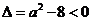 ,即
,即 时,对一切
时,对一切 都有
都有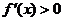 ,此时
,此时 在
在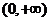 上是增函数。
上是增函数。
②
当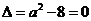 ,即
,即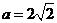 时,仅对
时,仅对 有
有 ,对其余的
,对其余的 都有
都有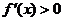 ,此时
,此时 在
在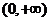 上也是增函数。
上也是增函数。
③
当 ,即
,即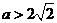 时,
时,
方程 有两个不同的实根
有两个不同的实根 ,
,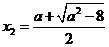 ,
,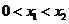 .
.
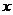 |
 |
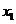 |
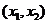 |
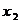 |
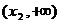 |
 |
+ |
0 |
_ |
0 |
+ |
 |
单调递增 |
极大 |
单调递减 |
极小 |
单调递增 |
此时 在
在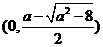 上单调递增, 在
上单调递增, 在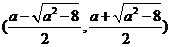 是上单调递减, 在
是上单调递减, 在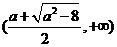 上单调递增.
上单调递增.
11.(2009广东卷理)(本小题满分14分)
已知二次函数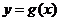 的导函数的图像与直线
的导函数的图像与直线 平行,且
平行,且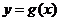 在
在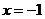 处取得极小值
处取得极小值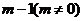 .设
.设 .
.
(1)若曲线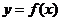 上的点
上的点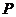 到点
到点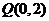 的距离的最小值为
的距离的最小值为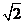 ,求
,求 的值;
的值;
(2) 如何取值时,函数
如何取值时,函数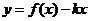 存在零点,并求出零点.
存在零点,并求出零点.
解:(1)依题可设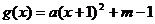 (
( ),则
),则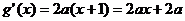 ;
;
又 的图像与直线
的图像与直线 平行
平行 
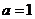
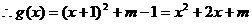 ,
,  ,
,
设 ,则
,则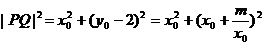 21世纪教育网
21世纪教育网 

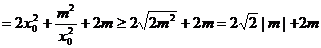
当且仅当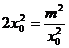 时,
时, 取得最小值,即
取得最小值,即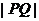 取得最小值
取得最小值
当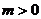 时,
时, 解得
解得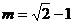
当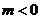 时,
时, 解得
解得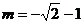
(2)由 (
( ),得
),得

当 时,方程
时,方程 有一解
有一解 ,函数
,函数 有一零点
有一零点 ;
;
当 时,方程
时,方程 有二解
有二解 ,
,
若 ,
, ,
,
函数 有两个零点
有两个零点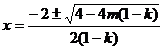 ,即
,即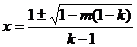 ;
;
若 ,
, ,
,
函数 有两个零点
有两个零点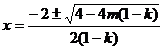 ,即
,即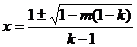 ;
;
当 时,方程
时,方程 有一解
有一解 ,
,  ,
,
函数 有一零点
有一零点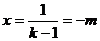
综上,当 时, 函数
时, 函数 有一零点
有一零点 ;
;
当 (
( ),或
),或 (
( )时,
)时,
函数 有两个零点
有两个零点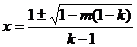 ;
;
当 时,函数
时,函数 有一零点
有一零点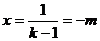 .
.
10.设函数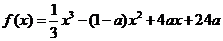 ,其中常数a>1
,其中常数a>1
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若当x≥0时,f(x)>0恒成立,求a的取值范围。21世纪教育网
解析:本题考查导数与函数的综合运用能力,涉及利用导数讨论函数的单调性,第一问关键是通过分析导函数,从而确定函数的单调性,第二问是利用导数及函数的最值,由恒成立条件得出不等式条件从而求出的范围。
解: (I) 21世纪教育网
21世纪教育网
由 知,当
知,当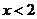 时,
时,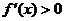 ,故
,故 在区间
在区间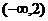 是增函数;
是增函数;
当 时,
时, ,故
,故 在区间
在区间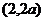 是减函数;
是减函数;
当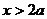 时,
时,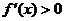 ,故
,故 在区间
在区间 是增函数。
是增函数。
综上,当 时,
时, 在区间
在区间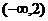 和
和 是增函数,在区间
是增函数,在区间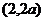 是减函数。
是减函数。
(II)由(I)知,当 时,
时, 在
在 或
或 处取得最小值。
处取得最小值。
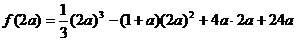
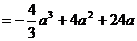
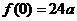
由假设知21世纪教育网
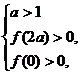 即
即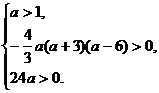 解得 1<a<6
解得 1<a<6
故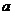 的取值范围是(1,6)
的取值范围是(1,6)
9.(2009山东卷文)(本小题满分12分)
已知函数 ,其中
,其中
(1) 当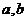 满足什么条件时,
满足什么条件时, 取得极值?
取得极值?
(2) 已知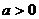 ,且
,且 在区间
在区间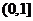 上单调递增,试用
上单调递增,试用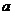 表示出
表示出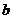 的取值范围.
的取值范围.
解: (1)由已知得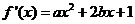 ,令
,令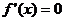 ,得
,得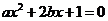 ,
,
 要取得极值,方程
要取得极值,方程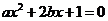 必须有解,
必须有解,
所以△ ,即
,即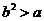 , 此时方程
, 此时方程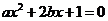 的根为
的根为
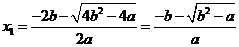 ,
,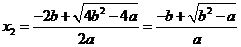 ,
,
所以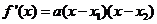
当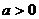 时,
时,
|
x |
(-∞,x1) |
x 1 |
(x1,x2) |
x2 |
(x2,+∞) |
|
f’(x) |
+ |
0 |
- |
0 |
+ |
|
f (x) |
增函数 |
极大值 |
减函数 |
极小值 |
增函数 |
所以 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
当 时,
时,
|
x |
(-∞,x2) |
x 2 |
(x2,x1) |
x1 |
(x1,+∞) |
|
f’(x) |
- |
0 |
+ |
0 |
- |
|
f (x) |
减函数 |
极小值 |
增函数 |
极大值 |
减函数 |
所以 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
综上,当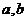 满足
满足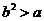 时,
时,  取得极值.
取得极值.
(2)要使 在区间
在区间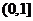 上单调递增,需使
上单调递增,需使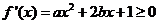 在
在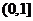 上恒成立.
上恒成立.
即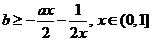 恒成立, 所以
恒成立, 所以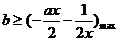
设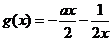 ,
, ,
,
令 得
得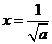 或
或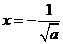 (舍去),
(舍去),
当 时,
时,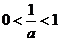 ,当
,当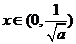 时
时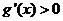 ,
,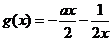 单调增函数;
单调增函数;
当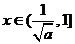 时
时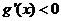 ,
,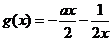 单调减函数,
单调减函数,
所以当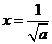 时,
时,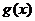 取得最大,最大值为
取得最大,最大值为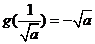 .
.
所以
当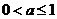 时,
时,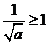 ,此时
,此时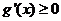 在区间
在区间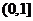 恒成立,所以
恒成立,所以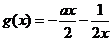 在区间
在区间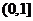 上单调递增,当
上单调递增,当 时
时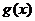 最大,最大值为
最大,最大值为 ,所以
,所以
综上,当 时,
时,  ; 当
; 当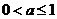 时,
时, 
[命题立意]:本题为三次函数,利用求导的方法研究函数的极值、单调性和函数的最值,函数在区间上为单调函数,则导函数在该区间上的符号确定,从而转为不等式恒成立,再转为函数研究最值.运用函数与方程的思想,化归思想和分类讨论的思想解答问题.
8.(2009山东卷理)(本小题满分12分)
两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧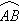 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在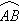 的中点时,对城A和城B的总影响度为0.065.
的中点时,对城A和城B的总影响度为0.065.
(1)将y表示成x的函数;
(11)讨论(1)中函数的单调性,并判断弧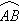 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
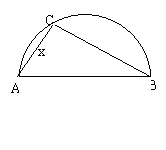 解法一:(1)如图,由题意知AC⊥BC,
解法一:(1)如图,由题意知AC⊥BC,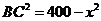 ,
,
其中当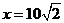 时,y=0.065,所以k=9
时,y=0.065,所以k=9
所以y表示成x的函数为
(2)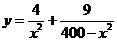 ,
,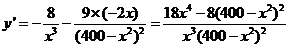 ,令
,令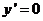 得
得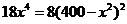 ,所以
,所以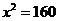 ,即
,即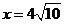 ,当
,当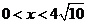 时,
时, 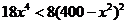 ,即
,即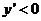 所以函数为单调减函数,当
所以函数为单调减函数,当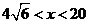 时,
时, 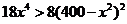 ,即
,即 所以函数为单调增函数.所以当
所以函数为单调增函数.所以当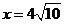 时, 即当C点到城A的距离为
时, 即当C点到城A的距离为 时, 函数
时, 函数 有最小值.
有最小值.
解法二: (1)同上.
(2)设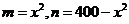 ,
,
则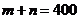 ,
,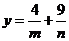 ,所以
,所以
 当且仅当
当且仅当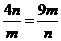 即
即 时取”=”.
时取”=”.
下面证明函数 在(0,160)上为减函数, 在(160,400)上为增函数.
在(0,160)上为减函数, 在(160,400)上为增函数.
设0<m1<m2<160,则
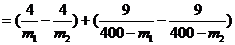
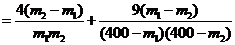
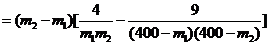
 ,
,
因为0<m1<m2<160,所以4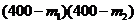 >4×240×240
>4×240×240
9 m1m2<9×160×160所以 ,
,
所以 即
即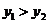 函数
函数 在(0,160)上为减函数.
在(0,160)上为减函数.
同理,函数 在(160,400)上为增函数,设160<m1<m2<400,则
在(160,400)上为增函数,设160<m1<m2<400,则

因为1600<m1<m2<400,所以4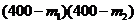 <4×240×240, 9 m1m2>9×160×160
<4×240×240, 9 m1m2>9×160×160
所以 ,
,
所以 即
即 函数
函数 在(160,400)上为增函数.
在(160,400)上为增函数.
所以当m=160即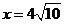 时取”=”,函数y有最小值,
时取”=”,函数y有最小值,
所以弧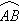 上存在一点,当
上存在一点,当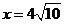 时使建在此处的垃圾处理厂对城A和城B的总影响度最小.
时使建在此处的垃圾处理厂对城A和城B的总影响度最小.
[命题立意]:本题主要考查了函数在实际问题中的应用,运用待定系数法求解函数解析式的 能力和运用换元法和基本不等式研究函数的单调性等问题.
7.(2009江苏卷)(本小题满分16分)
设 为实数,函数
为实数,函数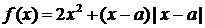 .
.
(1)若 ,求
,求 的取值范围;
的取值范围;
(2)求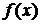 的最小值;
的最小值;
(3)设函数 ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式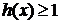 的解集.
的解集.
[解析]本小题主要考查函数的概念、性质、图象及解一元二次不等式等基础知识,考查灵活运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力。满分16分
(1)若 ,则
,则
(2)当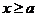 时,
时,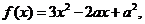
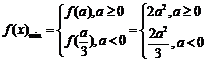
当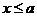 时,
时,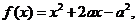
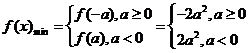
综上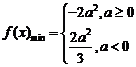
(3)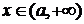 时,
时,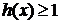 得
得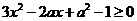 ,
,
当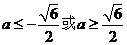 时,
时, ;
;
当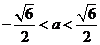 时,△>0,得:
时,△>0,得: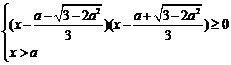
讨论得:当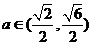 时,解集为
时,解集为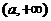 ;
;
当 时,解集为
时,解集为 ;
;
当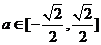 时,解集为
时,解集为 .
.
6.(2009北京理)(本小题共13分)
设函数
(Ⅰ)求曲线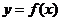 在点
在点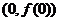 处的切线方程;
处的切线方程;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)若函数 在区间
在区间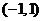 内单调递增,求
内单调递增,求 的取值范围.
的取值范围.
21世纪教育网 [解析]本题主要考查利用导数研究函数的单调性和极值、解不等式等基础知识,考查综合分析和解决问题的能力.
(Ⅰ)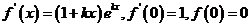 ,
,
曲线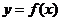 在点
在点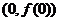 处的切线方程为
处的切线方程为 .
.
(Ⅱ)由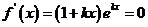 ,得
,得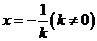 ,
,
若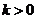 ,则当
,则当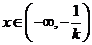 时,
时, ,函数
,函数 单调递减,
单调递减,
当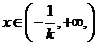 时,
时, ,函数
,函数 单调递增,
单调递增,
若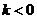 ,则当
,则当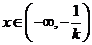 时,
时, ,函数
,函数 单调递增,
单调递增,
当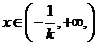 时,
时, ,函数
,函数 单调递减,
单调递减,
(Ⅲ)由(Ⅱ)知,若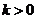 ,则当且仅当
,则当且仅当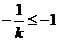 ,
,
即 时,函数
时,函数
 内单调递增,
内单调递增,
若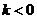 ,则当且仅当
,则当且仅当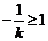 ,
,
即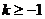 时,函数
时,函数
 内单调递增,
内单调递增,
综上可知,函数
 内单调递增时,
内单调递增时, 的取值范围是
的取值范围是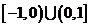 .
.
5.(2009北京文)(本小题共14分)
设函数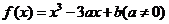 .
.
(Ⅰ)若曲线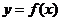 在点
在点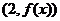 处与直线
处与直线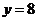 相切,求
相切,求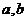 的值;
的值;
(Ⅱ)求函数 的单调区间与极值点.
的单调区间与极值点.
[解析]本题主要考查利用导数研究函数的单调性和极值、解不等式等基础知识,考查综合分析和解决问题的能力.
(Ⅰ)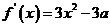 ,
,
∵曲线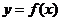 在点
在点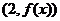 处与直线
处与直线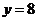 相切,
相切,
∴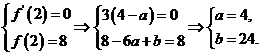
(Ⅱ)∵ ,
,
当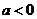 时,
时, ,函数
,函数 在
在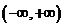 上单调递增,
上单调递增,
此时函数 没有极值点.
没有极值点.
当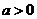 时,由
时,由 ,
,
当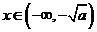 时,
时, ,函数
,函数 单调递增,
单调递增,
当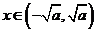 时,
时, ,函数
,函数 单调递减,
单调递减,
当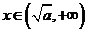 时,
时, ,函数
,函数 单调递增,
单调递增,
∴此时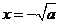 是
是 的极大值点,
的极大值点,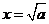 是
是 的极小值点.
的极小值点.
4.(2009浙江文)(本题满分15分)已知函数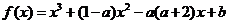
 .
.
(I)若函数 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是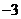 ,求
,求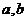 的值;
的值;
(II)若函数 在区间
在区间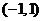 上不单调,求
上不单调,求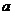 的取值范围.
的取值范围.
解析:(Ⅰ)由题意得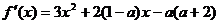
又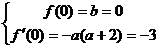 ,解得
,解得 ,
, 或
或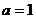
(Ⅱ)函数 在区间
在区间 不单调,等价于
不单调,等价于
导函数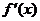 在
在 既能取到大于0的实数,又能取到小于0的实数
既能取到大于0的实数,又能取到小于0的实数
即函数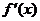 在
在 上存在零点,根据零点存在定理,有
上存在零点,根据零点存在定理,有
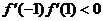 , 即:
, 即: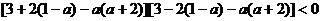
整理得: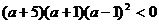 ,解得
,解得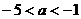
3.(2009浙江理)(本题满分14分)已知函数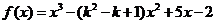 ,
,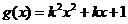 ,
,
其中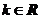 .21世纪教育网
.21世纪教育网
(I)设函数 .若
.若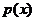 在区间
在区间 上不单调,求
上不单调,求 的取值范围;
的取值范围;
(II)设函数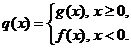 是否存在
是否存在 ,对任意给定的非零实数
,对任意给定的非零实数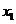 ,存在惟一
,存在惟一
的非零实数 (
(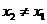 ),使得
),使得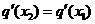 成立?若存在,求
成立?若存在,求 的值;若不存
的值;若不存
在,请说明理由.
解析:(I)因 ,
,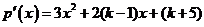 ,因
,因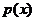 在区间
在区间 上不单调,所以
上不单调,所以 在
在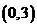 上有实数解,且无重根,由
上有实数解,且无重根,由 得
得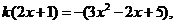 21世纪教育网
21世纪教育网
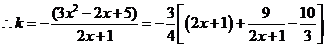 ,令
,令 有
有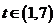 ,记
,记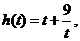 则
则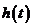 在
在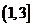 上单调递减,在
上单调递减,在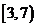 上单调递增,所以有
上单调递增,所以有 ,于是
,于是 ,得
,得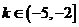 ,而当
,而当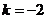 时有
时有 在
在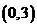 上有两个相等的实根
上有两个相等的实根 ,故舍去,所以
,故舍去,所以 ;21世纪教育网
;21世纪教育网
(II)当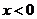 时有
时有 ;
;
当 时有
时有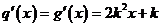 ,因为当
,因为当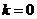 时不合题意,因此
时不合题意,因此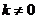 ,
,
下面讨论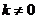 的情形,记A
的情形,记A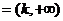 ,B=
,B=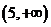 (ⅰ)当
(ⅰ)当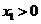 时,
时,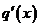 在
在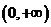 上单调递增,所以要使
上单调递增,所以要使 成立,只能
成立,只能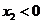 且
且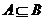 ,因此有
,因此有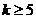 ,(ⅱ)当
,(ⅱ)当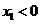 时,
时,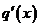 在
在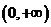 上单调递减,所以要使
上单调递减,所以要使 成立,只能
成立,只能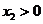 且
且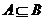 ,因此
,因此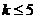 ,综合(ⅰ)(ⅱ)
,综合(ⅰ)(ⅱ)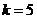 ;
;
当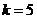 时A=B,则
时A=B,则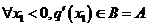 ,即
,即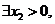 使得
使得 成立,因为
成立,因为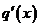 在
在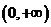 上单调递增,所以
上单调递增,所以 的值是唯一的;
的值是唯一的;
同理,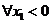 ,即存在唯一的非零实数
,即存在唯一的非零实数 ,要使
,要使 成立,所以
成立,所以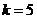 满足题意.21世纪教育网
满足题意.21世纪教育网
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com