
21.
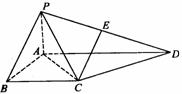 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD为直角梯形,
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD为直角梯形,
∠ABC=∠BAD=90°,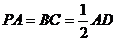 .
.
(1)求证:平面PAC⊥平面PCD;
(2)在棱PD上是否存在一点E,使CE//平面PAB?
若存在,请确定E点的位置;若不存在,请说明理由
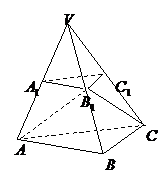
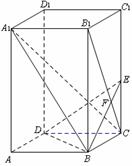
20.如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,
⑴求证:A1C⊥平面BDE;
⑵求A1B与平面BDE所成角的正弦值。
19. 如图6所示,在长方体ABCD-A1B1C1D1中,AB = BC = 1,
BB1 = 2,正是棱CC1上的点,且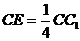
(1)求三棱锥C-BED的体积;
(2)求证:A1C⊥平面BDE.
.
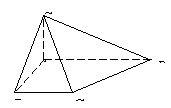
18.如图,已知DA⊥平面ABE,四边形ABCD是边长为2的正方形,
在△ABE中,AE=1,BE=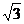
(1)证明:平面ADE⊥平面BCE;
(2)求二面角B-AC-E的余弦值。
17. 如图,在四棱锥
如图,在四棱锥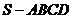 中,
中,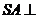 平面
平面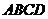 ,
,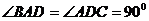 ,
,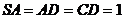 ,
,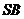 与平面
与平面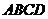 所成角的大小是
所成角的大小是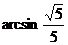 .
.
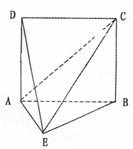 (1)求四棱锥
(1)求四棱锥 的体积;
的体积;
(2)求异面直线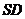 与
与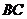 所成角的大小.
所成角的大小.
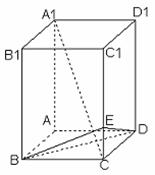
15.球面上三点A、B、C,已知AB=1,AC=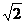 ,BC=
,BC=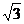 ,若球心到截面ABC的距离等于球半径的一半,则球的表面积为
,若球心到截面ABC的距离等于球半径的一半,则球的表面积为
16将正方形ABCD沿对角线BD折成直二面角,给出下列四个结论:①AC⊥BD;②AB,CD所成角为60°;③△ADC为等边三角形;④AB与平面BCD所成角为60°。其中真命题是 。(填命题序号)
14.在三棱锥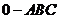 中,三条棱
中,三条棱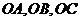 两两互相垂直,且
两两互相垂直,且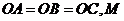 是
是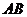 边的中点,则
边的中点,则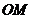 与平面
与平面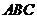 所成角的大小是________________(用反三角函数表示)
所成角的大小是________________(用反三角函数表示)
13.从正方体的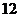 条棱所在的直线中任取
条棱所在的直线中任取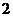 条,这
条,这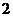 条直线是异面直线的概率是_____(结果用分数表示)
条直线是异面直线的概率是_____(结果用分数表示)
12.四面体的六条棱中,有五条棱长都等于a,则该四面体的体积的最大值
A.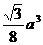 B.
B.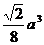 C.
C. 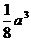 D.
D.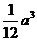
11.过球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的表面积的比为
A. B. C. D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com