
7.下列四个函数中,不满足f()≤的是 (A) f(x) = ax + b (B) f(x) = x2 + ax + b (C) f(x) = (D) f(x) = - lnx
6.下列函数中不是奇函数的是 (A) y = (B) y = (C) y = (D) y = log a
5.已知x + x – 1 = 3,则 +
+ 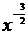 的值为
(A) 3 (B)
2 (C)
4 (D)
-4
的值为
(A) 3 (B)
2 (C)
4 (D)
-4
4.若y = x + b与y = ax + 3互为反函数,则 a + b = (A) -2 (B) 2 (C) 4 (D) -10
3.命题p:“a、b是整数”,是命题q:“ x 2 + ax + b = 0 有且仅有整数解”的 (A) 充分不必要条件 (B) 必要不充分条件
(C) 充要条件 (D) 既不充分也不必要条件
2.ax2 + 2x + 1 = 0至少有一个负实根的充要条件是(一上43页B组6) (A)0<a≤1 (B) a<1 (C) a≤1 (D) 0<a≤1或a<0
1.如果X = ,那么(一上40页例1(1)) (A) 0 Í X (B) {0} Î X (C) F Î X (D) {0} Í X
开放的行为给上面三个简单的问题注入了新的活力,推陈出“新”、自己给自己出题是人自我意识的回归。开放的过程说白了就是探索的过程。以下以抛物线的焦点弦问题为例来看开放问题的探索。
(例4)已知抛物线 ,过焦点F的直线与抛物线相交于A(x1,y1),B(x1,y)两点,P(x0,y0)是线段AB的中点;抛物线的准线为l,分别过点A、B、P作x轴的平行线,依次交l于M、N、Q,连接FM、FN、FQ、AQ和BQ(如图)
,过焦点F的直线与抛物线相交于A(x1,y1),B(x1,y)两点,P(x0,y0)是线段AB的中点;抛物线的准线为l,分别过点A、B、P作x轴的平行线,依次交l于M、N、Q,连接FM、FN、FQ、AQ和BQ(如图)
(1)试尽可能地找出:
(a)点A、B、P的纵、横6个坐标所满足的等量关系;
(b)图中各线段的垂直关系.
(2)如果允许引辅助线,你还能发现哪些结论?
(分析与解)(1)(a)点A、B、P的6个坐标x1,y1;x2,y2;x0,y0之间至少有下列等量关系:
①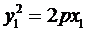 ②
②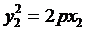 ③
③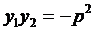 ④
④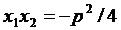
⑤ ⑥
⑥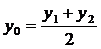
“所有的画都是以只有3种原色的方式构成的。每当我们把某样东西说成是新的的时候,我们真正谈论的是现有元素独特的存在方式。”具备对“封闭”题“开放”的意识的学生,事实上就有了创造意识,这种意识驱动下的实践自然会使创造力得以发展;同时,随着高考命题改革的进一步深入,我想这样的“开放”会在高考中更显示其生命力。
2.季节性服饰在当季即将到来之时,价格呈上升趋势,设某服饰开始时定价为10元,并且每周(7天)涨价2元,5周后开始保持20元的价格平稳销售,10周后当季即将过去,平均每周削价2元,直到20周末该服饰不再销售。
函数概念的形成,一般是从具体的实例开始的,但在学习函数时,往往较少考虑实际意义,本题旨在通过学生根据自己的知识经验给出函数的实际解释,体会到数学概念的一般性和背景的多样性。这是对问题理解上的开放。
(例3)由圆x2+y2=4上任意一点向x轴作垂线。求垂线夹在圆周和x轴间的线段中点的轨迹方程。(《高中平面解析几何》复习参考题二第11题)(答案:x2/4+y2=1)
问题本身开放:先从问题中分解出一些主要“组件”,如:A、“圆x2+y2=4”;B、“x轴”;C、“线段中点”等。然后对这些“组件”作特殊化、一般化等处理便可获得新问题。
对A而言,圆作为一种特殊的曲线,我们将其重新定位在“曲线”上,那么曲线又可分解成大小、形状和位置三要素,于是改变条件A(大小或形状或位置)就可使问题向三个方向延伸。
如改变位置,将A写成“(x-a)2+(y-b)2=4”,即可得所求的轨迹方程为(x-a)2+(2y-b)2=4;再将其特殊化(取a=0),并进行新的组合便有问题:圆x2+(y-b)2=4与椭圆x2+(2y-b)2=4有怎样的位置关系?试说明理由。
简解:解方程组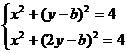 得 y=0 或y=2b/3
得 y=0 或y=2b/3
当y=0时,x2+b2=4,
(1)若b<-2或 b>2,圆与椭圆没有公共点;
(2)若b=±2,圆与椭圆恰有一个公共点;
(3)若 -2<b<2,圆与椭圆恰有二个公共点。
当y=2b/3时,x2+b2/9=4,
(1)若b<-6或b>6,圆与椭圆没有公共点;
(2)若b=±6,圆与椭圆恰有一个公共点;
(3)若-6<b<6,圆与椭圆恰有二个公共点。
综上所述,圆x2+(y-b)2=4与椭圆x2+(2y-b)2=4,当b<-6或b>6时没有公共点;当b=±6时恰有一个公共点;当-6<b<-2或b=0或2<b<6时恰有二个公共点;当b=±2时恰有三个公共点;当-2<b<0或0<b<2时恰有四个公共点。
上面的解法是从“数”着手,也可以从“形”着手分析。
再进一步延伸,得:当b>6时,圆x2+(y-b)2=4上的点到椭圆x2+(2y-b)2=4上的点的最大距离是多少?这个问题的解决是对数形结合、等价转化等思想的进一步强化。
对B而言,它是一条特殊的直线,通过对其位置的变更可产生许多有意义的问题;而C是一种特殊的线段分点,同样可以使其推广到一般,若对由此产生的结果继续研究就会发现以往的一些会考、高考试题。
有了开放的意识,加上方法指导,开放才会成为可能。开放问题的构建主要从两个方面进行,其一是问题本身的开放而获得新问题,其二是问题解法的开放而获得新思路。根据创造的三要素:“结构、关系、顺序”,我们可以为学生构建由“封闭”题“开放”的如下框图模式:

(例1)已知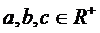 ,并且
,并且 求证
求证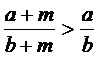 (《高中代数》下册第12页例7)
(《高中代数》下册第12页例7)
除教材介绍的方法外,根据目标的结构特征,改变一下考察问题的角度,或同时对目标的结构作些调整、重新组合,可获得如下思路:两点(b,a)、(-m,-m)的连线的斜率大于两点(b,a)、(0,0)的连线的斜率;b个单位溶液中有a个单位溶质,其浓度小于加入m个单位溶质后的浓度;在数轴上的原点和坐标为1的点处,分别放置质量为m、a的质点时质点系的重心,位于分别放置质量为m、b的质点时质点系的重心的左侧等。
(例2)用实际例子说明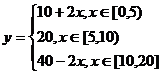 所表示的意义
所表示的意义
给变量赋予不同的内涵,就可得出函数不同的解释,我们从物理和经济两个角度出发给出实例。
1.X表示时间(单位:s),y表示速度(单位:m/s),开始计时后质点以10/s的初速度作匀加速运动,加速度为2m/s2,5秒钟后质点以20/s的速度作匀速运动,10秒钟后质点以-2m/s2的加速度作匀减速运动,直到质点运动到20秒末停下。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com