
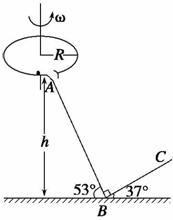
9.(07·山东理综)如图所示,一水平圆盘绕过圆心的竖直轴转动,圆盘边缘有一质量m=1.0 kg的小滑块.当圆盘转动的角速度达到某一数值时,滑块从圆盘边缘滑落,经光滑的过渡圆管进入轨道ABC.已知AB段斜面倾角为53°,BC段斜面倾角为37°,滑块与圆盘及斜面间的动摩擦因数均为μ=0.5,A点离B点所在水平面的高度h=1.2 m.滑块在运动过程中始终未脱离轨道,不计在过渡圆管处和B点的机械能损失,最大静摩擦力近似等于滑动摩擦力,取g=10 m/s2,sin 37°=0.6,cos 37°=0.8.
(1)若圆盘半径R=0.2 m,当圆盘的角速度多大时,滑块从圆盘上滑落?
(2)若取圆盘所在平面为零势能面,求滑块到达B点时的机械能.
(3)从滑块到达B点时起,经0.6 s正好通过C点,求BC之间的距离.
答案 (1)5 rad/s (2)-4 J (3)0.76 m
解析 (1)滑块在圆盘上做圆周运动时,静摩擦力充当向心力,根据牛顿第二定律,可得:
μmg=mω2R
代入数据解得:ω=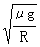 =5 rad/s?
=5 rad/s?
(2)滑块在A点时的速度:vA=ωR=1 m/s?
从A到B的运动过程由动能定理得
mgh-μmgcos
53° ·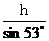 =
= mvB2-
mvB2- mvA2
mvA2
在B点时的机械能:EB= mvB2-mgh=-4 J
mvB2-mgh=-4 J
(3)滑块在B点时的速度:vB=4 m/s?
滑块沿BC段向上运动时的加速度大小:
a1=g(sin 37°+μcos 37°)=10 m/s2
返回时的加速度大小
a2=g(sin 37°-μcos 37°)=2 m/s2
BC间的距离:sBC=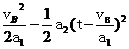 =0.76 m
=0.76 m
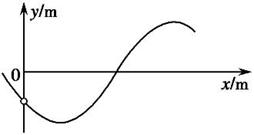
8.(07·上海·5)在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=2.5cos(kx+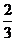 π)(单位: m),式中k=1 m-1.将一光滑小环套在该金属杆上,并从x=0处以v0=5
m/s的初速度沿杆向下运动,取重力加速度g=10 m/s2..则当小环运动到x=
π)(单位: m),式中k=1 m-1.将一光滑小环套在该金属杆上,并从x=0处以v0=5
m/s的初速度沿杆向下运动,取重力加速度g=10 m/s2..则当小环运动到x=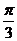 m时的速度大小v=
m/s;该小环在x轴方向最远能运动到x=
m处. 答案
m时的速度大小v=
m/s;该小环在x轴方向最远能运动到x=
m处. 答案 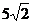
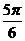
解析 当x=0时,y1=2.5 cos 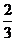 π=-1.25
m,当x=
π=-1.25
m,当x=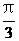 时,y2=2.5 cos π=-2.5 m,由此可知,小环下落的高度为Δy=y1-y2=-1.25 m-(-2.5) m=1.25 m由动能定理得:mgΔy=
时,y2=2.5 cos π=-2.5 m,由此可知,小环下落的高度为Δy=y1-y2=-1.25 m-(-2.5) m=1.25 m由动能定理得:mgΔy= mv2-
mv2- mv02,代入数值得:v=
mv02,代入数值得:v=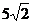 m/s.当小环速度为零时,设上升的高度为h,由动能定理得:-mgh=0-
m/s.当小环速度为零时,设上升的高度为h,由动能定理得:-mgh=0- mv02,则h=
mv02,则h=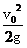 =1.25 m,故当y=0时,小环速度为零,所以有2.5cos
(kx+
=1.25 m,故当y=0时,小环速度为零,所以有2.5cos
(kx+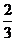 π)=0,得x=
π)=0,得x=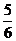 π
π
7.(07·天津理综·15)如图所示,物体A静止在光滑的水平面上,A的左边固定有轻质弹簧,与A质量相等的物体B以速度v向A运动并与弹簧发生碰撞.A、B始终沿同一直线运动,则A、B组成的系统动能损失最大的时刻是 ( )
 A.A开始运动时
A.A开始运动时
B.A的速度等于v时
C.B的速度等于零时
D.A和B的速度相等时
答案 D
解析 A、B两物体碰撞过程中动量守恒,当A、B两物体速度相等时,系统动能损失最大,损失的动能转化成弹簧的弹性势能.
6.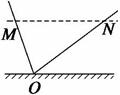 (07·山东理综·20)如图所示,光滑轨道MO和ON底端对接且ON=2MO,M、N两点高度相同.小球自M点由静止自由滚下,忽略小球经过O点时的机械能损失,以v、S、a、E0、分别表示小球的速度、位移、加速度和动能四个物理量的大小.下列图象中能正确反映小球自M点到N点运动过程的是 ( )
(07·山东理综·20)如图所示,光滑轨道MO和ON底端对接且ON=2MO,M、N两点高度相同.小球自M点由静止自由滚下,忽略小球经过O点时的机械能损失,以v、S、a、E0、分别表示小球的速度、位移、加速度和动能四个物理量的大小.下列图象中能正确反映小球自M点到N点运动过程的是 ( )
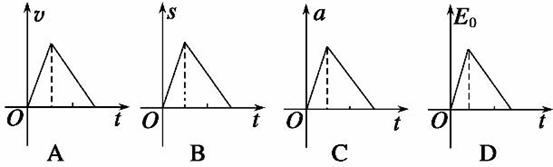
答案 A?
解析 从M到O,v1=a1t,从O到N,v2=v1-a2t=(a1-a2)t,v与t是一次函数关系,所以A正确;从M到O,s= a1t2,则s与t的图象是抛物线,所以B错;从M到O和从O到N,加速度是常数,所以C错;从M到O,Ek=
a1t2,则s与t的图象是抛物线,所以B错;从M到O和从O到N,加速度是常数,所以C错;从M到O,Ek= mv12=
mv12= ma12t2,所以D错.
ma12t2,所以D错.
5.(07·广东理科基础·7)人骑自行车下坡,坡长l=500 m,坡高h=8 m,人和车总质量为100 kg,下坡时初速度为4 m/s,人不踏车的情况下,到达坡底时车速为10 m/s,g取10 m/s2,则下坡过程中阻力所做的功为 ( )
A.-4 000 J B.-3 800 J
C.-5 000 J 200 J
答案 B
解析 下坡过程中,重力做功WG=mgh=100×10×8 J=8 000 J,支持力不做功,阻力做功W,由动能定理得:WG+W?= mvt2-mv02,代入数据得:W=-3 800 J.
mvt2-mv02,代入数据得:W=-3 800 J.
4.(07·广东·4)机车从静止开始沿平直轨道做匀加速运动,所受的阻力始终不变,在此过程中,
下列说法正确的是 ( )
A.机车输出功率逐渐增大
B.机车输出功率不变
C.在任意两相等的时间内,机车动能变化相等
D.在任意两相等的时间内,机车动量变化的大小相等
答案 AD
解析 机车在匀加速运动中,牵引力不变,而速度越来越大,由P=Fv知,其输出功率逐渐增大,在任意相等的时间内,机车位移越来越大,其合外力不变,则合外力做的功越来越多,故机车动能变化变大;由动量定理可知,合外力的冲量等于动量的变化量.
3.(07·全国卷Ⅱ·20)假定地球、月球都静止不动,用火箭从地球沿地月连线向月球发射一探测器.假定探测器在地球表面附近脱离火箭.用W表示探测器从脱离火箭处飞到月球的过程中克服地球引力做的功,用Ek表示探测器脱离火箭时的动能,若不计空气阻力,则 ( )
A.Ek必须大于或等于W,探测器才能到达月球
B.Ek小于W,探测器也可能到达月球
C.Ek= W,探测器一定能到达月球
W,探测器一定能到达月球
D.Ek= W,探测器一定不能到达月球
W,探测器一定不能到达月球
答案 BD
解析 假设没有月球的吸引力,当探测器的初动能为W时,探测器刚好到达月球,当探测器的动能Ek<W时,因为有月球的吸引力,探测器也可能到达月球.地球的质量约是月球质量的6倍,探测器从地球到月球要克服地球引力做功W,在这个过程中月球对探测器做的功一定小于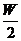 ,所以当Ek=
,所以当Ek=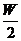 时,探测器一定不能到达月球.
时,探测器一定不能到达月球.
2.(07·广东理科基础·9)一人乘电梯从1楼到20楼,在此过程中经历了先加速,后匀速,再减速的运动过程,则电梯支持力对人做功情况是
( )
A.加速时做正功,匀速时不做功,减速时做负功 B.加速时做正功,匀速和减速时做负功
C.加速和匀速时做正功,减速时做负功 D.始终做正功
答案 D
解析 在加速、匀速、减速的过程中,支持力与人的位移方向始终相同,所以支持力始终对人做正功。
1.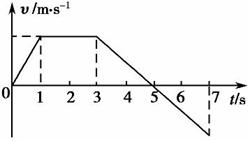 (07·上海·12)物体沿直线运动的v-t关系如图所示,已知在第1秒内合外力对物体做的功为W,则 ( )
(07·上海·12)物体沿直线运动的v-t关系如图所示,已知在第1秒内合外力对物体做的功为W,则 ( )
A.从第1秒末到第3秒末合外力做功为4 W
B.从第3秒末到第5秒末合外力做功为-2 W
C.从第5秒末到第7秒末合外力做功为W
D.从第3秒末到第4秒末合外力做功为-0.75 W
答案 CD
解析 由v-t图象可以看出,若第1 s末速度为v1=v0则第3 s末速度为v3=v0,第4 s末速度为v4=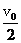 第5 s末速度为v5=0第7 s末速度为v7=-v0,因为第1 s内合外力做功为W,则由动能定理可知:W=
第5 s末速度为v5=0第7 s末速度为v7=-v0,因为第1 s内合外力做功为W,则由动能定理可知:W= mv02第1 s末到第3 s末合外力做功W1=
mv02第1 s末到第3 s末合外力做功W1= mv32-
mv32- mv02=0;第3 s末到第5 s末合外力做功W2=
mv02=0;第3 s末到第5 s末合外力做功W2= mv52-
mv52- mv32=-
mv32=- mv02=-W;第5 s末到第7 s末合外力做功W3=
mv02=-W;第5 s末到第7 s末合外力做功W3= mv72-
mv72- mv52=
mv52= mv02=W;第3 s末到第4 s末合外力做功为W4=
mv02=W;第3 s末到第4 s末合外力做功为W4=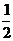 mv42-
mv42-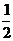 mv32=
mv32= m(
m(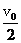 )2-
)2- mv02=-
mv02=-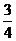 ×
× mv02=-0.75W.上所述,C、D选项正确.
mv02=-0.75W.上所述,C、D选项正确.
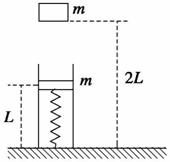
23.(08·重庆理综·24)如图中有一个竖直固定在地面的透气圆筒,筒中有一个劲度为k的轻弹簧,其下端固定,上端连接一质量为m的薄滑块,圆筒内壁涂有一层新型智能材料--ER流体,它对滑块的阻力可调.起初,滑块静止,ER流体对其阻力为0,弹簧的长度为L.现有一质量也为m的物体从距地面2L处自由落下,与滑块碰撞后粘在一起向下运动.为保证滑块做匀减速运动,且下移距离为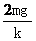 时速度减为0,ER流体对滑块的阻力须随滑块下移而变.试求(忽略空气阻力):
时速度减为0,ER流体对滑块的阻力须随滑块下移而变.试求(忽略空气阻力):
(1)下落物体与滑块碰撞过程中系统损失的机械能;
(2)滑块向下运动过程中加速度的大小;
(3)滑块下移距离d时ER流体对滑块阻力的大小。
答案 (1) mgL (2)
mgL (2)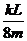 (3)mg+
(3)mg+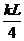 -kd
-kd
解析 (1)设物体下落末速度为v0,由机械能守恒定律mgL= mv02,得v0=
mv02,得v0=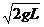 ,
,
设碰后共同速度为v1,由动量守恒定律2mv1=mv0,得v1=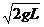 .碰撞过程中系统损
.碰撞过程中系统损
 失的机械能为ΔE=
失的机械能为ΔE= mv02-
mv02- ×2mv12=
×2mv12= mgL.
mgL.
(2)设加速度大小为a,有2as=v12,得a=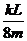 .
.
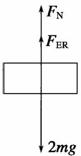
(3)设弹簧弹力为FN,ER流体对滑块的阻力为FER,受力分析如图所示:
FN+FER-2mg=2ma,FN=kx,x=d+mg/k,得FER=mg+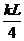 -kd.
-kd.
三年高考·集训(2005-2007)
题组一
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com