
2.共振
当驱动力的频率跟物体的固有频率相等时,受迫振动的振幅最大,这种现象叫共振。
要求会用共振解释现象,知道什么情况下要利用共振,什么情况下要防止共振。
⑴利用共振的有:共振筛、转速计、微波炉、打夯机、跳板跳水、打秋千……
⑵防止共振的有:机床底座、航海、军队过桥、高层建筑、火车车厢……
例5. 把一个筛子用四根弹簧支起来,筛子上装一个电动偏心轮,它每转一周,给筛子一个驱动力,这就做成了一个共振筛。不开电动机让这个筛子自由振动时,完成20次全振动用15s;在某电压下,电动偏心轮的转速是88r/min。已知增大电动偏心轮的电压可以使其转速提高,而增加筛子的总质量可以增大筛子的固有周期。为使共振筛的振幅增大,以下做法正确的是
A.降低输入电压 B.提高输入电压
C.增加筛子质量 D.减小筛子质量
解:筛子的固有频率为f固=4/3Hz,而当时的驱动力频率为f驱=88/60Hz,即f固< f驱。为了达到振幅增大,应该减小这两个频率差,所以应该增大固有频率或减小驱动力频率。本题应选AD。
1.受迫振动
物体在驱动力(既周期性外力)作用下的振动叫受迫振动。
⑴物体做受迫振动的频率等于驱动力的频率,与物体的固有频率无关。
⑵物体做受迫振动的振幅由驱动力频率和物体的固有频率共同决定:两者越接近,受迫振动的振幅越大,两者相差越大受迫振动的振幅越小。
2.单摆。
⑴单摆振动的回复力是重力的切向分力,不能说成是重力和拉力的合力。在平衡位置振子所受回复力是零,但合力是向心力,指向悬点,不为零。
⑵当单摆的摆角很小时(小于5°)时,单摆的周期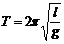 ,与摆球质量m、振幅A都无关。其中l为摆长,表示从悬点到摆球质心的距离,要区分摆长和摆线长。
,与摆球质量m、振幅A都无关。其中l为摆长,表示从悬点到摆球质心的距离,要区分摆长和摆线长。
 ⑶小球在光滑圆弧上的往复滚动,和单摆完全等同。只要摆角足够小,这个振动就是简谐运动。这时周期公式中的l应该是圆弧半径R和小球半径r的差。
⑶小球在光滑圆弧上的往复滚动,和单摆完全等同。只要摆角足够小,这个振动就是简谐运动。这时周期公式中的l应该是圆弧半径R和小球半径r的差。
⑷摆钟问题。单摆的一个重要应用就是利用单摆振动的等时性制成摆钟。在计算摆钟类的问题时,利用以下方法比较简单:在一定时间内,摆钟走过的格子数n与频率f成正比(n可以是分钟数,也可以是秒数、小时数……),再由频率公式可以得到:
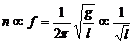
 例2. 已知单摆摆长为L,悬点正下方3L/4处有一个钉子。让摆球做小角度摆动,其周期将是多大?
例2. 已知单摆摆长为L,悬点正下方3L/4处有一个钉子。让摆球做小角度摆动,其周期将是多大?
 解:该摆在通过悬点的竖直线两边的运动都可以看作简谐运动,周期分别为
解:该摆在通过悬点的竖直线两边的运动都可以看作简谐运动,周期分别为 和
和 ,因此该摆的周期为 :
,因此该摆的周期为 :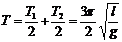
例3. 固定圆弧轨道弧AB所含度数小于5°,末端切线水平。两个相同的小球a、b分别从轨道的顶端和正中由静止开始下滑,比较它们到达轨道底端所用的时间和动能:ta__tb,Ea__2Eb。
 解:两小球的运动都可看作简谐运动的一部分,时间都等于四分之一周期,而周期与振幅无关,所以ta= tb;从图中可以看出b小球的下落高度小于a小球下落高度的一半,所以Ea>2Eb。
解:两小球的运动都可看作简谐运动的一部分,时间都等于四分之一周期,而周期与振幅无关,所以ta= tb;从图中可以看出b小球的下落高度小于a小球下落高度的一半,所以Ea>2Eb。
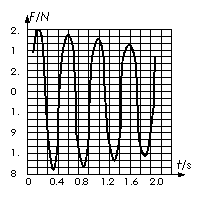
例4. 将一个力电传感器接到计算机上,可以测量快速变化的力。用这种方法测得的某单摆摆动过程中悬线上拉力大小随时间变化的曲线如右图所示。由此图线提供的信息做出下列判断:①t=0.2s时刻摆球正经过最低点;②t=1.1s时摆球正处于最高点;③摆球摆动过程中机械能时而增大时而减小;④摆球摆动的周期约是T=0.6s。上述判断中正确的是
A.①③ B.②④ C.①② D.③④
解:注意这是悬线上的拉力图象,而不是振动图象。当摆球到达最高点时,悬线上的拉力最小;当摆球到达最低点时,悬线上的拉力最大。因此①②正确。从图象中看出摆球到达最低点时的拉力一次比一次小,说明速率一次比一次小,反映出振动过程摆球一定受到阻力作用,因此机械能应该一直减小。在一个周期内,摆球应该经过两次最高点,两次最低点,因此周期应该约是T=1.2s。因此答案③④错误。本题应选C。
1.弹簧振子
⑴周期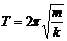 ,与振幅无关,只由振子质量和弹簧的劲度决定。
,与振幅无关,只由振子质量和弹簧的劲度决定。
⑵可以证明,竖直放置的弹簧振子的振动也是简谐运动,周期公式也是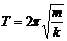 。这个结论可以直接使用。
。这个结论可以直接使用。
⑶在水平方向上振动的弹簧振子的回复力是弹簧的弹力;在竖直方向上振动的弹簧振子的回复力是弹簧弹力和重力的合力。
 例1. 如图所示,质量为m的小球放在劲度为k的轻弹簧上,使小球上下振动而又始终未脱离弹簧。⑴最大振幅A是多大?⑵在这个振幅下弹簧对小球的最大弹力Fm是多大?
例1. 如图所示,质量为m的小球放在劲度为k的轻弹簧上,使小球上下振动而又始终未脱离弹簧。⑴最大振幅A是多大?⑵在这个振幅下弹簧对小球的最大弹力Fm是多大?
解:该振动的回复力是弹簧弹力和重力的合力。在平衡位置弹力和重力等大反向,合力为零;在平衡位置以下,弹力大于重力,F- mg=ma,越往下弹力越大;在平衡位置以上,弹力小于重力,mg-F=ma,越往上弹力越小。平衡位置和振动的振幅大小无关。因此振幅越大,在最高点处小球所受的弹力越小。极端情况是在最高点处小球刚好未离开弹簧,弹力为零,合力就是重力。这时弹簧恰好为原长。
⑴最大振幅应满足kA=mg, A=
⑵小球在最高点和最低点所受回复力大小相同,所以有:Fm-mg=mg,Fm=2mg
3.从总体上描述简谐运动的物理量
振动的最大特点是往复性或者说是周期性。因此振动物体在空间的运动有一定的范围,用振幅A来描述;在时间上则用周期T来描述完成一次全振动所须的时间。
⑴振幅A是描述振动强弱的物理量。(一定要将振幅跟位移相区别,在简谐运动的振动过程中,振幅是不变的而位移是时刻在改变的)
⑵周期T是描述振动快慢的物理量。(频率f=1/T 也是描述振动快慢的物理量)周期由振动系统本身的因素决定,叫固有周期。任何简谐振动都有共同的周期公式: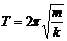 (其中m是振动物体的质量,k是回复力系数,即简谐运动的判定式F= -kx中的比例系数,对于弹簧振子k就是弹簧的劲度,对其它简谐运动它就不再是弹簧的劲度了)。
(其中m是振动物体的质量,k是回复力系数,即简谐运动的判定式F= -kx中的比例系数,对于弹簧振子k就是弹簧的劲度,对其它简谐运动它就不再是弹簧的劲度了)。
2.几个重要的物理量间的关系
要熟练掌握做简谐运动的物体在某一时刻(或某一位置)的位移x、回复力F、加速度a、速度v这四个矢量的相互关系。
⑴由定义知:F∝x,方向相反。
⑵由牛顿第二定律知:F∝a,方向相同。
⑶由以上两条可知:a∝x,方向相反。
⑷v和x、F、a之间的关系最复杂:当v、a同向(即 v、 F同向,也就是v、x反向)时v一定增大;当v、a反向(即 v、 F反向,也就是v、x同向)时,v一定减小。
1.定义
物体在跟偏离平衡位置的位移大小成正比,并且总指向平衡位置的回复力的作用下的振动,叫简谐运动。表达式为:F= -kx
⑴简谐运动的位移必须是指偏离平衡位置的位移。也就是说,在研究简谐运动时所说的位移的起点都必须在平衡位置处。
⑵回复力是一种效果力。是振动物体在沿振动方向上所受的合力。
⑶“平衡位置”不等于“平衡状态”。平衡位置是指回复力为零的位置,物体在该位置所受的合外力不一定为零。(如单摆摆到最低点时,沿振动方向的合力为零,但在指向悬点方向上的合力却不等于零,所以并不处于平衡状态)
⑷F=-kx是判断一个振动是不是简谐运动的充分必要条件。凡是简谐运动沿振动方向的合力必须满足该条件;反之,只要沿振动方向的合力满足该条件,那么该振动一定是简谐运动。
3.利用图象解题:
|
|
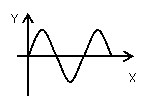
振动图象 |
波动图象 |
|
研究对象 |
 一个质点 一个质点 |
 多个质点 多个质点 |
|
坐标 |
|
|
|
物理意义 |
一个质点的位移随时间变化的情况 |
同一时刻各质点离开平衡位置的情况 |
|
直接物理量 |
A 、 T |
A λ |
|
图象变化 |
随时间延续 |
随时间波形平移 |
①用振动求波动:
例1:一列简谐波沿直线传播,位于此直线上相距为2米的A、B两点的振动图象如图所示。以知这列波的波长大于1米,则此波的波长为 米;波速为 米/秒。

②波的多值问题:
例2:一根张紧的水平弹性绳上的a 、b 两点相距14米,b点在a点右方。当一列简谐波沿此绳向右传播时,若a点的位移达到正的极大时,b点的位移恰为零,且向下运动。经过1.00秒, a 点的位移为零,且向下运动,而b点位移恰达到负的极大,则这列简谐波的波速
可能是:A、4.67m/s ; B、6m/s C、10m/s D、14m/s
附:
2. 摆钟校准:
例:有一挂钟,其摆锤的振动可看成单摆,在正常运动时,摆动周期为2秒。现因调整不当,使该钟每天快3分钟,试求摆长比正常摆长缩短了多少?
解: 摆锤摆动越快,表的指针走的越快,所以表的指针转动的快
慢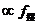 :
:
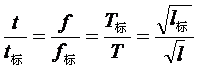 或 =
或 =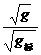
1. 等效单摆:
例1:在一升降机中悬有一单摆,以加速度 向上做匀加速度运动,则此单摆的摆动周期为多少?
向上做匀加速度运动,则此单摆的摆动周期为多少?

例2:已知小车中有一单摆,求小车匀速或以加速度 向右运动时,单摆的摆动周期?
向右运动时,单摆的摆动周期?
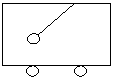
 例3:求单摆的振动周期:
例3:求单摆的振动周期:

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com