
16、解:(1)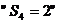 即前四次中有三次出现“√”,一次出现“×”,
即前四次中有三次出现“√”,一次出现“×”,
所以概率为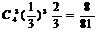 。
。
2)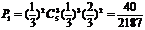 ,
,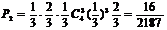 所求概率为
所求概率为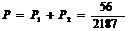 。
。
21.设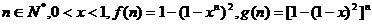 ,试比较
,试比较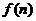 与
与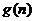 的大小,并证明你的结论.
的大小,并证明你的结论.
解答:
20.如图,直四棱柱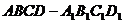 的高为3,底面是边长为4的菱形
,且
的高为3,底面是边长为4的菱形
,且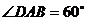 ,
,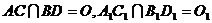 ,
,
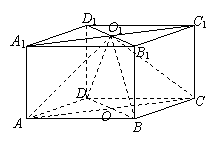 (1)求证:平面
(1)求证:平面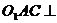 平面
平面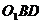 ;
;
(2)求二面角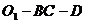 的大小.
的大小.
19.甲、乙两人参加一次英语口语考试,已知在编号为1-10的10道试题中,甲能答对编号为1-6的6道题,乙能答对编号为3-10的8道题,规定每位考生都从备选题中抽出3道试题进行测试,至少答对2道才算合格,(1)求甲答对试题数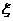 的概率分布及数学期望;
的概率分布及数学期望;
(2)求甲、乙两人至少有一人考试合格的概率.
18.在长方体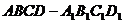 中,
中,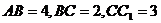 ,
,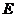 分
分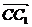 所成比为2,
所成比为2,
 (1)求点
(1)求点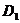 到平面
到平面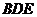 的距离;
的距离;
(2)求直线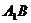 与平面
与平面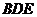 所成角的大小.
所成角的大小.
17.
 杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律。下图是一个11阶杨辉三角:
杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律。下图是一个11阶杨辉三角:
(1)求第20行中从左到右的第4个数;(2)若第n行中从左到右第14与第15个数的比为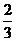 ,求n的值;(3)若n阶(包括0阶)杨辉三角的所有数的和;
,求n的值;(3)若n阶(包括0阶)杨辉三角的所有数的和;
(4)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35。显然,1+3+6+10+15=35。事实上,一般地有这样的结论:
第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数。
试用含有m、k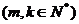 的数学公式表示上述结论,并给予证明。
的数学公式表示上述结论,并给予证明。
16.一种信号灯,只有符号“√”和“×”随机反复出现,每秒钟变化一次,每次变化只出现“√”和“×”两者之一,其中出现“√”的概率为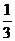 ,出现“×”的概率为
,出现“×”的概率为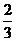 ,若第
,若第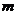 次出现“√”,记为
次出现“√”,记为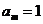 ,若第
,若第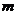 次出现“×”,则记为
次出现“×”,则记为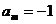 ,令
,令 ,(1)求
,(1)求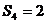 的概率;(2)求
的概率;(2)求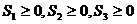 ,且
,且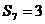 的概率.
的概率.
15.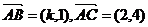 ,
,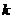 为满足
为满足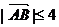 的一随机整数,则
的一随机整数,则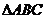 是
是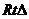 的概率是________.
的概率是________.
14.已知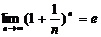 ,则
,则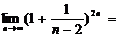
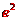
13.如图,A、B、C是球O的球面上三点,且OA、OB、OC
两两垂直,P是球O的大圆上BC弧上的中点,则直线AP与OB
所成角的弧度数是
.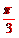
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com