2．不相等的向量是否一定不平行？(不一定)

1．平行向量是否一定方向相同？(不一定)

例1 判断下列命题是否正确，若不正确，请简述理由.　

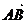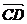①向量与是共线向量，则A、B、C、D四点必在一直线上；　

②单位向量都相等；　

③任一向量与它的相反向量不相等；　

④四边形ABCD是平行四边形的充要条件是＝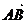

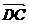
⑤模为0是一个向量方向不确定的充要条件；　

⑥共线的向量，若起点不同，则终点一定不同.

解：①不正确.共线向量即平行向量，只要求方向相同或相反即可，并不要求两个向量、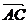在同一直线上.

②不正确.单位向量模均相等且为1，但方向并不确定.

③不正确.零向量的相反向量仍是零向量，但零向量与零向量是相等的.

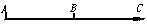④、⑤正确.⑥不正确.如图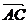与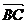共线，虽起点不同，但其终点却相同.

评述：本题考查基本概念，对于零向量、单位向量、平行向量、共线向量的概念特征及相互关系必须把握好.

例2下列命题正确的是(　　 )　

A.a与b共线，b与c共线，则a与c也共线　

B.任意两个相等的非零向量的始点与终点是一平行四边形的四顶点　

C.向量a与b不共线，则a与b都是非零向量　

D.有相同起点的两个非零向量不平行

解：由于零向量与任一向量都共线，所以A不正确；由于数学中研究的向量是自由向量，所以两个相等的非零向量可以在同一直线上，而此时就构不成四边形，根本不可能是一个平行四边形的四个顶点，所以B不正确；向量的平行只要方向相同或相反即可，与起点是否相同无关，所以D不正确；对于C，其条件以否定形式给出，所以可从其逆否命题来入手考虑，假若a与b不都是非零向量，即a与b至少有一个是零向量，而由零向量与任一向量都共线，可有a与b共线，不符合已知条件，所以有a与b都是非零向量，所以应选C.

评述：对于有关向量基本概念的考查，可以从概念的特征入手，也可以从反面进行考虑，要启发学生注意这两方面的结合

4．向量与有向线段的区别：

(1)向量是自由向量，只有大小和方向两个要素；与起点无关：只要大小和方向相同，则这两个向量就是相同的向量；

(2)有向线段有起点、大小和方向三个要素，起点不同，尽管大小和方向相同，也是不同的有向线段

3.实数与向量不能相加减，但实数与向量可以相乘.

初学向量的同学很可能认为一个实数与一个向量之间可进行加法或者减法，这是错误的.实数与向量之间不能相加减，但可相乘，相乘的意义就是几个相等向量相加.

2.向量不能比较大小

我们知道，长度相等且方向相同的两个向量表示相等向量，但是两个向量之间只有相等关系，没有大小之分，“对于向量a，b，a＞b，或a＜b”这种说法是错误的.

6.共线向量与平行向量关系：

平行向量就是共线向量，这是因为任一组平行向量都可移到同一直线上.

说明：(1)平行向量可以在同一直线上，要区别于两平行线的位置关系；

(2)共线向量可以相互平行，要区别于在同一直线上的线段的位置关系.

探究：1.对向量概念的理解

要深刻理解向量的概念，就要深刻理解有向线段这一概念.在线段AB的两个端点中，我们规定了一个顺序，A为起点，B为终点，我们就说线段AB具有射线AB的方向，具有方向的线段就叫做有向线段.通常有向线段的终点要画箭头表示它的方向，以A为起点，以B为终点的有向线段记为，需要学生注意的是：的字母是有顺序的，起点在前终点在后，所以我们说有向线段有三个要素：起点、方向、长度.

既有大小又有方向的量，我们叫做向量，有些向量既有大小、方向、作用点(起点)，比如力；有些向量只有大小、方向，比如位移、速度，我们现在所学的向量一般指后者.

5.相等向量定义：

长度相等且方向相同的向量叫相等向量.

说明：(1)向量a与b相等，记作a＝b；

(2)零向量与零向量相等；

(3)任意两个相等的非零向量，都可用同一条有向线段来表示，并且与有向线段的起点无关.

4.平行向量定义：

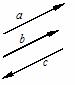①方向相同或相反的非零向量叫平行向量；

②我们规定0与任一向量平行.

说明：(1)综合①、②才是平行向量的完整定义；

(2)向量a、b、c平行，记作a∥b∥c.

3.零向量、单位向量概念：

①长度为0的向量叫零向量，记作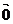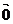的方向是任意的

注意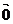与0的区别

②长度为1个单位长度的向量，叫单位向量.

说明：零向量、单位向量的定义都是只限制大小，不确定方向.