
18.(丁中)求与椭圆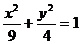 有公共顶点,且离心率为
有公共顶点,且离心率为 的双曲线方程.
的双曲线方程.
错解: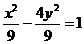
错因:忽视了椭圆的短轴上的两个顶点。
正解: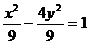 ,
,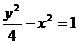
17.(丁中)已知点A(-2,-1)和B(2,3),圆C:x2+y2 = m2,当圆C与线段AB没有公共点时,求m的取值范围。
错解: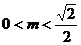 ,
,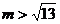
错因:将题中的实数m当成了圆的半径,误认为m>0。
正解: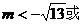
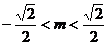
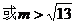 且
且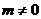
16.(一中)已知点N(1,2),过点N的直线交双曲线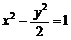 于A、B两点,且
于A、B两点,且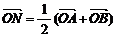
(1)求直线AB的方程;
(2)若过N的直线l交双曲线于C、D两点,且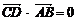 ,那么A、B、C、D四点是否共圆?为什么?
,那么A、B、C、D四点是否共圆?为什么?
解:(1)设直线AB: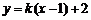 代入
代入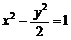 得
得
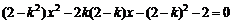 (*)
(*)
令A(x1,y1),B(x2,y2),则x1、x2是方程的两根
∴ 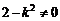 且
且 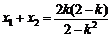
∵ 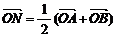 ∴ N是AB的中点
∴
∴ N是AB的中点
∴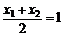
∴ 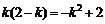 k = 1 ∴AB方程为:y
= x + 1
k = 1 ∴AB方程为:y
= x + 1
(2)将k = 1代入方程(*)得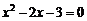
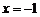 或
或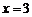
由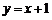 得
得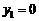 ,
,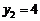
∴ 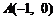 ,
,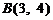
∵ 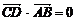 ∴ CD垂直平分AB ∴ CD所在直线方程为
∴ CD垂直平分AB ∴ CD所在直线方程为
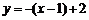 即
即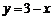 代入双曲线方程整理得
代入双曲线方程整理得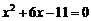
令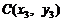 ,
,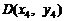 及CD中点
及CD中点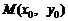
则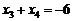 ,
,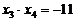 , ∴
, ∴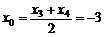 ,
, 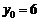
|CD| =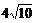 ,
,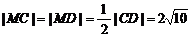
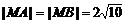 ,即A、B、C、D到M距离相等
,即A、B、C、D到M距离相等
∴ A、B、C、D四点共圆
15.(一中)如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且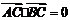 ,|BC|=2|AC|.
,|BC|=2|AC|.
 (I)建立适当的坐标系,求椭圆方程;
(I)建立适当的坐标系,求椭圆方程;
(II)如果椭圆上有两点P、Q,使∠PCQ的平分线垂直于AO,证明:存在实数λ,使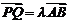 .
.
解:(I)以O为原点,OA为X轴建立直角坐标系,设A(2,0),则椭圆方程为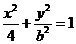
∵O为椭圆中心,∴由对称性知|OC|=|OB|
又∵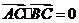 , ∴AC⊥BC
, ∴AC⊥BC
又∵|BC|=2|AC| ∴|OC|=|AC|
∴△AOC为等腰直角三角形
∴点C的坐标为(1,1) ∴点B的坐标为(-1,-1)
将C的坐标(1,1)代入椭圆方程得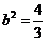 ,
,
则求得椭圆方程为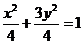
(II)由于∠PCQ的平分线垂直于OA(即垂直于x轴),不妨设PC的斜率为k,则QC的斜率为-k,因此PC、QC的直线方程分别为y=k(x-1)+1,y=-k(x-1)+1
由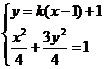 得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0 *)
得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0 *)
∵点C(1,1)在椭圆上,
∴x=1是方程(*)的一个根,∴xP•1=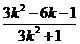 即xP=
即xP=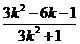
同理xQ=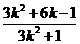
∴直线PQ的斜率为 (定值)
(定值)
又∠ACB的平分线也垂直于OA
∴直线PQ与AB的斜率相等(∵kAB=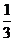 )
)
∴向量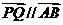 ,即总存在实数
,即总存在实数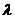 ,使
,使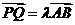 成立.
成立.
14.(城西中学)设F1、F2是双曲线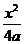 -
-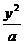 =1(a>0)的两个焦点
=1(a>0)的两个焦点
⑴若点P在双曲线上,且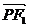 ·
·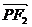 =0,|
=0,|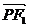 |·|
|·|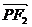 |=2,求双曲线的方程。
|=2,求双曲线的方程。
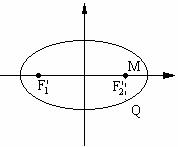
⑵设曲线C是以⑴中的双曲线的顶点为焦点,焦点为顶点的椭圆,若F1’、F2’分别是其左右 焦点,点Q是椭圆上任一点,M(2,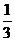 )是平面上一点,求|QM|+|QF1’|的最大值。
)是平面上一点,求|QM|+|QF1’|的最大值。
正确答案:⑴因为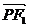 ·
·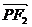 =0,∴
=0,∴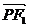 ⊥
⊥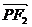 依题意
依题意
 |
|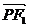 |2+|
|2+|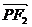 |2=|
|2=| |2 ①
|2 ①
|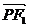 |+|
|+|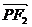 |=2 ②
|=2 ②
||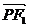 |-|
|-|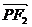 ||=4
||=4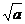 ③
③
①-③2:2|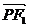 |·|
|·|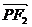 |=4a,将②代入得a=1,
|=4a,将②代入得a=1,
所以双曲线的方程为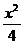 -y2=1
-y2=1
⑵由⑴及题意可得C的方程为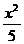 +y2=1,所以|QF1’|+|QF2’|=2
+y2=1,所以|QF1’|+|QF2’|=2
且F1’(-2,0),F2’(2,0),显然M点在椭圆内部。
所以|QM|+|QF1’|=|QM|+2 -|QF2’|≤2
-|QF2’|≤2 +|MF2’|
+|MF2’|
如图当|QM|-|QF2’|=|MF2’|时 |QM|-|QF2’|的值最大
所以|QM|+|QF1’|的最大值为2 +
+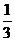
错因:第二问的转化出错。
13.(磨中)设椭圆的中心在坐标原点,长轴在x轴上,离心率e=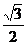 ,已知点P(0,
,已知点P(0,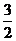 )
)
到这个椭圆上的点的最远距离为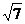 ,求这个椭圆的方程,并求椭圆上到点P的距离等于
,求这个椭圆的方程,并求椭圆上到点P的距离等于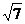 的点坐标。
的点坐标。
正确答案: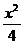 +y2=1
+y2=1
错语原因:①利用相切的条件求解设有理论依据
②求最值时忽视了b的范围而没有加以讨论,导致解题过程出错。
12.(磨中)设抛物线y2=2Px(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥x轴,证明直线AC经过原点O。
正确答案:见2001年全国高考理19题
错误原因:设直线斜率为k,考虑到一般情况,而忽视了特殊情况。
11.(搬中) 已知椭圆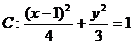 ,F为它的右焦点,直线
,F为它的右焦点,直线 过原点交椭圆C于A、B两点。求
过原点交椭圆C于A、B两点。求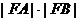 是否存在最大值或最小值?若不存在,说明理由。
是否存在最大值或最小值?若不存在,说明理由。
错解 设A、B两点坐标分别为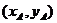 、
、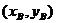
因为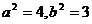
所以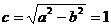
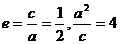
又椭圆中心为(1,0),右准线方程为x=5
所以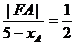
即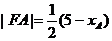
同理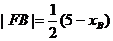
所以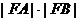
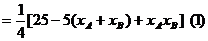
设直线 的方程为y=kx,代入椭圆方程得
的方程为y=kx,代入椭圆方程得
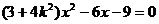
所以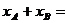
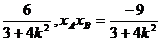
代入(1)式得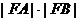
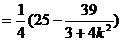
所以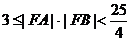
所以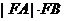 |有最小值3,无最大值。
|有最小值3,无最大值。
剖析 上述错解过程忽视了过原点斜率不存在的直线,当 的斜率不存在时,有
的斜率不存在时,有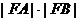
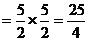
所以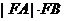 有最小值为
3,最大值为25/4
有最小值为
3,最大值为25/4
10.(搬中)已知双曲线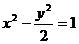 ,问过点A(1,1)能否作直线
,问过点A(1,1)能否作直线 ,使
,使 与双曲线交于P、Q两点,并且A为线段PQ的中点?若存在,求出直线
与双曲线交于P、Q两点,并且A为线段PQ的中点?若存在,求出直线 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
错解 设符合题意的直线 存在,并设
存在,并设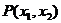 、
、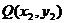
则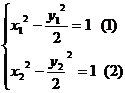
(1)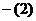 得
得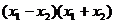
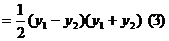
因为A(1,1)为线段PQ的中点,
所以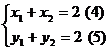
将(4)、(5)代入(3)得
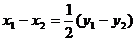
若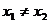 ,则直线
,则直线 的斜率
的斜率
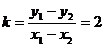
所以符合题设条件的直线 存在。
存在。
其方程为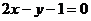
剖析 在(3)式成立的前提下,由(4)、(5)两式可推出(6)式,但由(6)式不能推出(4)(5)两式,故应对所求直线进行检验,上述错解没有做到这一点,故是错误的。
应在上述解题的基础上,再由
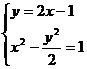
得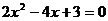
根据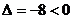 ,说明所求直线不存在。
,说明所求直线不存在。
9. (搬中)椭圆中心是坐标原点,长轴在x轴上,离心率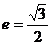 ,已知点P(
,已知点P(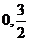 )到椭圆上的点最远距离是
)到椭圆上的点最远距离是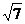 ,求这个椭圆的方程。
,求这个椭圆的方程。
错解 设所求椭圆方程为
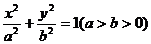
因为
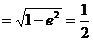
所以a=2b
于是椭圆方程为
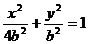
设椭圆上点M(x,y)到点P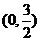 的距离为d,
的距离为d,
则: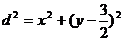
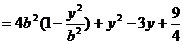
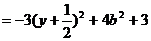
所以当 时,
时,
有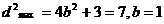
所以所求椭圆方程为

剖析 由椭圆方程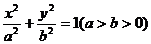
得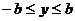
由(1)式知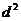 是y的二次函数,
是y的二次函数,
其对称轴为
上述错解在于没有就对称轴在区间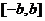 内或外进行分类,
内或外进行分类,
其正确应对f(y)=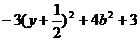 的最值情况进行讨论:
的最值情况进行讨论:
(1)当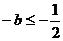 ,即
,即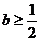 时
时
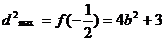 =7
=7
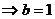 ,方程为
,方程为
(2)当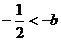 ,
,
即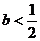 时,
时,
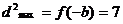
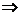
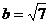
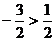 ,与
,与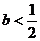 矛盾。
矛盾。
综上所述,所求椭圆方程为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com