
373. 定点P不在△ABC所在平面内,过P作平面α,使△ABC的三个顶点到α的距离相等,这样的平面共有 ( )
(A)1个 (B)2个 (C)3个 (D)4个
解析:D
过P作一个与AB,AC都平行的平面,则它符合要求;设边AB,BC,CA的中点分别为E,F,G,则平面PEF符合要求;同理平面PFG,平面PGE符合要求
372. 在正方体ABCD-A1B1C1D1中,若E是A1C1的中点,则直线CE垂直于 ( )
(A)AC (B)BD (C)A1D (D)A1D1
解析:(B)
BD⊥AC,BD⊥CC1,∴BD⊥平面A1ACC1,∴BD⊥CE.
371. 若两直线a与b异面,则过a且与b垂直的平面 ( )
 (A)有且只有一个 (B)可能存在也可能不存在
(A)有且只有一个 (B)可能存在也可能不存在
(C)有无数多个 (D)一定不存在
(B)
解析:若存在,则a⊥b,而由条件知,a不一定与b垂直.
370. 点P在线段AB上,且AP∶PB=1∶2,若A,B到平面α的距离分别为a,b,求点P到平面α的距离.
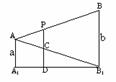 解析:(1)A,B在平面α的同侧时,P平面α的距离为
解析:(1)A,B在平面α的同侧时,P平面α的距离为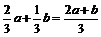 ;
;
(2)A,B在平面α的异侧时,P平面α的距离为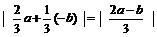 .
.
点评 一是画图时,只要画出如右上图的平面图形即可,无需画出空间图形;二是对第(2)种情形,若以平面为“水平面”,在其上方的点高度为正,在其下方的点高度为负,则第(2)种情形的结论,就是将(1)结论中的b改为(-b),而无需再画另一图形加以求解.
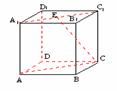
369. 如图,在正方体ABCD-A1B1C1D1中,M为棱CC1的中点,AC交BD于点O,求证:A1O⊥平面MBD.
解析:要证A1O⊥平面MBD,只要在平面MBD内找到两条相交直线与A1O都垂直,首先想到DB,先观察 A1O垂直DB吗?
方法1:发现A1O平分DB,想到什么?(△A1DB是否为等腰三角形)
∵A1D=A1B,DO=OB,∴A1O⊥DB.
方法2:A1O⊥DB吗?即DB⊥A1O吗?DB垂直包含A1O的平面吗?(易见DB⊥平面A1ACC1)
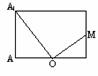 再观察A1O垂直何直线?DM?BM?因这两条直线与A1O均异面,故难以直接观察,平面MDB中还有何直线?易想到MO,因MO与A1O相交,它们在同一平面内,这是一个平几问题,可画出平几图进行观察.
再观察A1O垂直何直线?DM?BM?因这两条直线与A1O均异面,故难以直接观察,平面MDB中还有何直线?易想到MO,因MO与A1O相交,它们在同一平面内,这是一个平几问题,可画出平几图进行观察.
证明 取CC1中点M,连结MO,∵DB⊥A1A,DB⊥AC,A1A∩AC=A,∴DB⊥平面A1ACC1,而A1O 平面A1ACC1,∴A1O⊥DB.在矩形A1ACC1中,∵tan∠AA1O=
平面A1ACC1,∴A1O⊥DB.在矩形A1ACC1中,∵tan∠AA1O=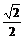 ,tan∠MOC=
,tan∠MOC=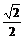 ,∴∠AA1O=∠MOC,则∠A1OA+∠MOC=90°,∴A1O⊥OM,∵OM∩DB=O,∴A1O⊥平面MBD.
,∴∠AA1O=∠MOC,则∠A1OA+∠MOC=90°,∴A1O⊥OM,∵OM∩DB=O,∴A1O⊥平面MBD.
368. 如图,在正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱B1C1,A1D1,D1D,AB的中点.
(1)求证:A1E⊥平面ABMN.
(2)平面直线A1E与MF所成的角.
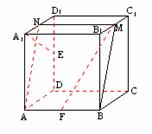 解析:(1)要证A1E⊥平面ABMN,只要在平面中找到两条相交直线与A1E都垂直,显然MN与它垂直,这是因为MN⊥平面A1ADD1,另一方面,AN与A1E是否垂直,这是同一个平面中的问题,只要画出平面几何图形,用平几知识解决.(2)为(1)的应用.
解析:(1)要证A1E⊥平面ABMN,只要在平面中找到两条相交直线与A1E都垂直,显然MN与它垂直,这是因为MN⊥平面A1ADD1,另一方面,AN与A1E是否垂直,这是同一个平面中的问题,只要画出平面几何图形,用平几知识解决.(2)为(1)的应用.
证明 (1)∵AB⊥平面A1ADD1,
而A1E 平面A1ADD1,
平面A1ADD1,
∴AB⊥A1E.在平面A1ADD1中,A1E⊥AN,
∵AN∩AB=A,∴A1E⊥平面ABMN.
解 (2)由(1)知A1E⊥平面ABMN,而MF 平面ABMN,∴A1E⊥MF,
平面ABMN,∴A1E⊥MF,
则A1E与MF所成的角为90°
367. 已知P为 ABCD所在平面外一点,M为PB的中点,求证:PD∥平面MAC.
ABCD所在平面外一点,M为PB的中点,求证:PD∥平面MAC.
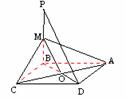 解析: 因M为PB的中点,连BD∩AC于O后,可将PD缩小平移到MO,可见MO为所求作的平行线.
解析: 因M为PB的中点,连BD∩AC于O后,可将PD缩小平移到MO,可见MO为所求作的平行线.
证明 连AC交BD于O,连MO,
则MO为△PBD的中位线,
∴PD∥MO,∵PD 平面MAC,MO平面MAC,
平面MAC,MO平面MAC,
∴PD∥平面MAC.
366. 在正方体ABCD-A1B1C1D1中,期棱长为a.
(1)求证BD⊥截面AB1C;
(2)求点B到截面AB1C的距离;
(3)求BB1与截面AB1C所成的角的余弦值。

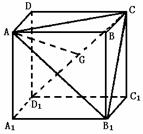
同理BD1⊥AB1.∴BD1⊥面ACB1.
(2)AB=BC=BB1 G为△AB1C的中心.AC=
G为△AB1C的中心.AC=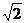 a
a
AG=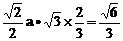 a
a
∴BG=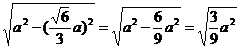 =
=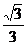 a
a
(3)∠BB1G为所求
cos∠BB1G=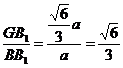
365. 设棱锥M-ABCD的底面是正方形,且MA=MD,MA⊥AB,如果ΔAMD的面积为1,试求能够放入这个棱锥的最大球的半径.
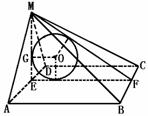
解析: ∵AB⊥AD,AB⊥MA,
∴AB⊥平面MAD,
由此,面MAD⊥面AC.
记E是AD的中点,
从而ME⊥AD.
∴ME⊥平面AC, ME⊥EF
设球O是与平面MAD、AC、平面MBC都相切的球.
不妨设O∈平面MEF,于是O是ΔMEF的内心.
设球O的半径为r,则r=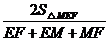
设AD=EF=a,∵SΔAMD=1.
∴ME=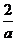 .MF=
.MF=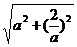 ,
,
r=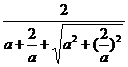 ≤
≤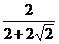 =
=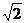 -1
-1
当且仅当a=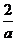 ,即a=
,即a=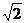 时,等号成立.
时,等号成立.
∴当AD=ME=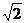 时,满足条件的球最大半径为
时,满足条件的球最大半径为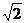 -1.
-1.
364. 在有阳光时,一根长为3米的旗轩垂直于水平地面,它的影长为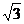 米,同时将一个半径为3米的球放在这块水平地面上,如图所示,求球的阴影部分的面积(结果用无理数表示).
米,同时将一个半径为3米的球放在这块水平地面上,如图所示,求球的阴影部分的面积(结果用无理数表示).
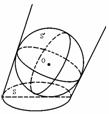
解析:由题意知,光线与地面成60°角,设球的阴影部分面积为S,垂直于光线的大圆面积为S′,则Scos30°=S′,并且S′=9π,所以S=6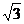 π(米2)
π(米2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com