
393.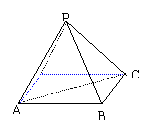 正四棱锥的一个对角面与一个侧面的面积之比为
正四棱锥的一个对角面与一个侧面的面积之比为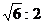 ,求侧面与底面所成的角的大小。
,求侧面与底面所成的角的大小。
解析:如图,正四棱锥P-ABCD的一个对角面△PAC。设棱锥的底面边长为a,高为h,斜高为h′,底面中心为O,连PO,则PO⊥底面ABCD,∴PO⊥AC,在△PAC中,AC=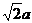 ,PO=h,
,PO=h,
 ∴
∴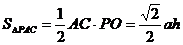
在△PBC中,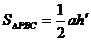 °
°
∴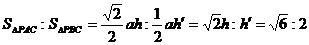
∴h:h′=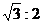 .
.
取BC中点E,连OE,PE,可证∠PEO即为侧面与底面所成两面角的平面角。
在Rt△POE中,sin∠PEO=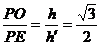 ,
,
∴∠PEO=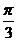 ,即侧面与底面所成的角为
,即侧面与底面所成的角为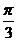 .
.
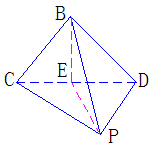
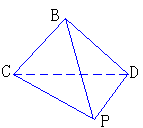
392. 如图,BCD是等腰直角三角形,斜边CD的长等于点P到BC的距离,D是P在平面BCD上的射影.(1)求PB与平面BCD所成角;(2)求BP与平面PCD所成的角
解析:(1)PD⊥平面BCD,∴BD是PB在平面BCD内的射影,∴∠PBD为PB与平面BCD所成角,BD⊥BC,由三垂线定理得BC⊥BD,∴BP=CD,设BC=a,则BD=a,BP=CD=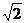 a∴在Rt△BPD中,
a∴在Rt△BPD中,
cos∠DBP=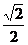 ∴∠DBP=45°, 即PB与平面BCD所成角为45°.
∴∠DBP=45°, 即PB与平面BCD所成角为45°.
(2)过B作BE⊥CD于E,连结PE,PD⊥平面BCD得PD⊥BE,∴BE⊥平面PCD,
 ∴∠BPE为BP与平面PCD所成的角,在Rt△BEP中,BE=
∴∠BPE为BP与平面PCD所成的角,在Rt△BEP中,BE=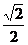 a, BP=
a, BP=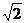 a,∴∠BPE=30°
即BP与平面PCD所成角为30°.
a,∴∠BPE=30°
即BP与平面PCD所成角为30°.
391. 如图,△ABC为锐角三角形,PA⊥平面ABC,A点在平面PBC上的射影为H,求:H不可能是△PBC的垂心.
解析: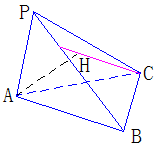 连结CH,则CH是AC在平面PBC内的射影,若H为垂心,则CH⊥PB,由三垂线定理得AC⊥PB,又PA⊥平面ABC,∴PA⊥AC,∴AC⊥平面PAB,从而AC⊥AB与△ABC为锐角三
连结CH,则CH是AC在平面PBC内的射影,若H为垂心,则CH⊥PB,由三垂线定理得AC⊥PB,又PA⊥平面ABC,∴PA⊥AC,∴AC⊥平面PAB,从而AC⊥AB与△ABC为锐角三
角形矛盾,故H不可能是垂心.
390. 已知α∩β=C,a∥b,a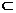 α,b
α,b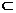 β,A
β,A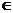 a,AE⊥b于E,AF⊥c于F,求证:a⊥EF
a,AE⊥b于E,AF⊥c于F,求证:a⊥EF
解析: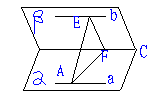 b∥a,b
b∥a,b ,a
,a α, ∴b∥α
α, ∴b∥α
又b β,α∩β=c ∴b∥c, 又AF⊥c ∴AF⊥b
β,α∩β=c ∴b∥c, 又AF⊥c ∴AF⊥b
又AE⊥b, AE∩AF=A ∴b⊥平面AEF a∥b ∴a⊥平面AEF
EF 平面AEF ∴a⊥EF
平面AEF ∴a⊥EF
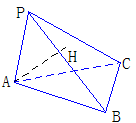
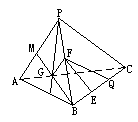
389. 设P点在正三角形ABC所在平面外,且AP,BP,CP两两垂直;又 是
是 的重心;
的重心;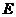 为
为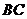 上一点,
上一点,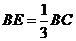 ;
;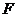 为
为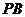 上一点,
上一点,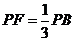 ;
;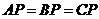 ,如图
,如图
(1)求证:GF⊥平面PBC;(2)求证:EF⊥BC。
解析:(1)连结BG并延长交PA于M.G为△ABP的重心
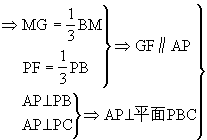
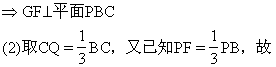
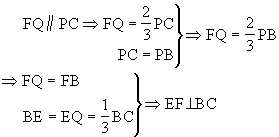
注 要充分注意平面几何中的知识(如本题中三角形重心性质,等腰三角形性质等)在证题中的运用。
388. 如图,在四棱锥P-ABCD中,侧面PCD是边长等于2cm的等边三角形,底面ABCD是面积为2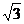 cm2的菱形,∠ADC是锐角.
cm2的菱形,∠ADC是锐角.
求证:PA⊥CD
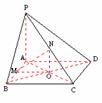
证明:设∠ADC=θ,则:由SABCD=2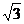 , CD=BC=AB=AD=2,易得θ=60°
, CD=BC=AB=AD=2,易得θ=60°
∴△ACD是等边三角形,取CD中点E连AE、PE,则AE⊥CD,PE⊥CD
AE⊥CD,PE⊥CD ∴CD⊥平面PAE ∴CD⊥PA
387. 如图,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.
(1)
 求证:MN⊥CD;
求证:MN⊥CD;
(2) 若∠PDA=45°,求证:MN⊥平面PCD.
证明 (1)连AC∩BD=O,连NO,MO,则NO∥PA.
∵PA⊥平面ABCD,∴NO⊥平面ABCD.
∵MO⊥AB,∴MN⊥AB,而CD∥AB,∴MN⊥CD;
(2)∵∠PDA=45°,∴PA=AD,
由△PAM≌△CBM得PM=CM,
∵N为PC中点,∴MN⊥PC.
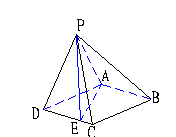 又MN⊥CD,PC∩CD=C,∴MN⊥平面PCD.
又MN⊥CD,PC∩CD=C,∴MN⊥平面PCD.
386. P是边长为a的六边形ABCDEF所成平面外一点,PA⊥AB,PA⊥AF,PA=a,则点P到边CD的距离是
解析:2a.
PA⊥平面ABCDEF,A到CD的距离为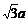 ,∴P到边CD的距离是2a
,∴P到边CD的距离是2a
385. △ABC在平面α内,∠C=90°,点P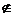 α,PA=PB=PC=7, AB=10, 则点P到平面α的距离等于
α,PA=PB=PC=7, AB=10, 则点P到平面α的距离等于
解析: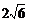 .
.
∵PA=PB=PC,∴P在平面α内的射影为△ABC的外心O,∵∠C=90°,∴O为AB的中点,∵AO=5,PA=7,∴PO=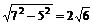
384. 直角三角形ABC的斜边AB在平面α内,直角顶点C在平面α外,C在平面α内的射影为C1,且C1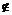 AB,则△C1AB为 ( )
AB,则△C1AB为 ( )
(A)锐角三角形 (B)直角三角形
(C)钝角三角形 (D)以上都不对
解析:(C)
∵C1A2+C1B2<CA2+CB2 =AB, ∴∠AC1B为钝角,则△C1AB为钝角三角形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com