
40. 如图,P是正角形ABC所在平面外一点,M、N分别是AB和PC的中点,且PA=PB=PC=AB=a。
(1)求证:MN是AB和PC的公垂线
(2)求异面二直线AB和PC之间的距离
解析:(1)连结AN,BN,∵△APC与△BPC是全等的正三角形,又N是PC的中点
∴AN=BN
又∵M是AB的中点,∴MN⊥AB
同理可证MN⊥PC
又∵MN∩AB=M,MN∩PC=N
∴MN是AB和PC的公垂线。
(2)在等腰在角形ANB中,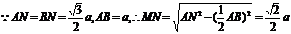
即异面二直线AB和PC之间的距离为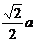 .
.
41空间有四个点,如果其中任意三个点都不在同一条直线上,那么经过其中三个点的平面 [ ]
A.可能有3个,也可能有2个 B.可能有4个,也可能有3个
C.可能有3个,也可能有1个 D.可能有4个,也可能有1个
解析:分类,第一类,四点共面,则有一个平面,第二类,四点不共面,因为没有任何三点共线,则任何三点都确定一个平面,共有4个。.
38. 在空间四边形ABCD中,AD=BC=2,E、F分别是AB、CD的中点,EF=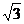 ,求AD与BC所成角的大小
,求AD与BC所成角的大小
(本题考查中位线法求异面二直线所成角)
解析:取BD中点M,连结EM、MF,则
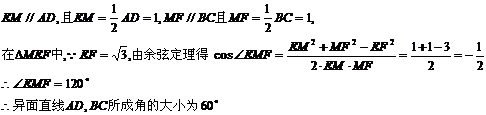
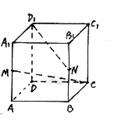 39. 如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱AA1和BB1的中点,求异面直线CM与D1N所成角的正弦值.(14分)
39. 如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱AA1和BB1的中点,求异面直线CM与D1N所成角的正弦值.(14分)
(本题考查平移法,补形法等求异面二直线所成角)
解析:取DD1中点G,连结BG,MG,MB,GC得矩形MBCG,记MC∩BG=0
则BG和MC所成的角为异面直线CM与D1N所成的角.
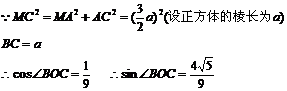
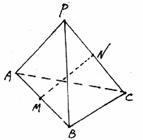 而CM与D1N所成角的正弦值为
而CM与D1N所成角的正弦值为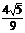
37. 已知:平面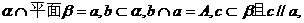
求证:b、c是异面直线
解析:反证法:若b与c不是异面直线,则b∥c或b与c相交
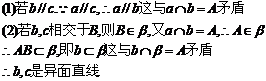
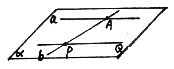
36. 已知△ABC三边所在直线分别与平面α交于P、Q、R三点,求证:P、Q、R三点共线。(12分)
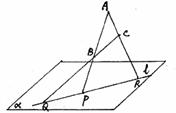 本题主要考查用平面公理和推论证明共线问题的方法
本题主要考查用平面公理和推论证明共线问题的方法
解析:∵A、B、C是不在同一直线上的三点
∴过A、B、C有一个平面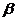
又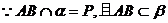
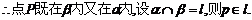
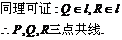
34. .用一个平面去截正方体。其截面是一个多边形,则这个多边形的边数最多是
.
解析:6条
 35. 已知:
35. 已知: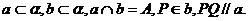
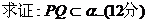
本题主要考查用平面公理和推论证明共面问题的方法.
解析:∵PQ∥a,∴PQ与a确定一个平面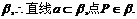
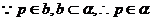
33..在空间四边形ABCD的边AB、BC、CD、DA上分别取E、F、G、H四点如果EF与HG交于点M,则 ( )
A.M一定在直线AC上
B.M一定在直线BD上
C.M可能在AC上,也可能在BD上
D.M不在AC上,也不在BD上
解析:∵平面ABC∩平面ACD=AC,先证M∈平面ABC,M∈平面ACD,从而M∈AC
A
32.两两相交的四条直线确定平面的个数最多的是 ( )
A.4个 B.5个 C.6个 D.8个
解析:C 如四棱锥的四个侧面,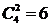 个。
个。
31.三个互不重合的平面把空间分成六个部份时,它们的交线有 ( )
A.1条 B.2条 C.3条 D.1条或2条
D
解析:分类:1)当两个平面平行,第三个平面与它们相交时,有两条交线; 2)当三个平面交于一条
直线时,有一条交线,故选D
30. 在正方体ABCD-A1B1C1D1中,E,F,G,H,M,N分别是正方体的棱 AB,BC,
AB,BC,
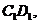
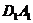 的中点,试证:E,F,G,H,M,N六点共面.
的中点,试证:E,F,G,H,M,N六点共面.
解析:∵EN//MF,∴EN与MF
共面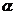 ,(2分)又∵EF//MH,∴EF和MH共面
,(2分)又∵EF//MH,∴EF和MH共面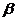 .(4分)∵不共线的三点E,F,M确定一个平面,(6分)∴平面
.(4分)∵不共线的三点E,F,M确定一个平面,(6分)∴平面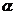 与
与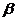 重合,∴点H
重合,∴点H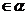 。(8分)同理点G
。(8分)同理点G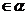 .(10分)故E,F,G,H,M,N六点共面.
.(10分)故E,F,G,H,M,N六点共面.
29. ⊿ABC是边长为2的正三角形,在⊿ABC所在平面外有一点P,PB=PC= ,PA=
,PA=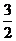 ,延长BP至D,使BD=
,延长BP至D,使BD=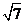 ,E是BC的中点,求AE和CD所成角的大小和这两条直线间的距离.
,E是BC的中点,求AE和CD所成角的大小和这两条直线间的距离.
解析:分别连接PE和CD,可证PE//CD,(2分)则∠PEA即是AE和CD所成角.(4分)在Rt⊿PBE中,
PB= ,BE=1,∴PE=
,BE=1,∴PE=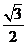 。在⊿AEP中,AE=
。在⊿AEP中,AE= ,
,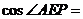
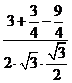 =
=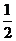 .
.
∴∠AEP=60º,即AE和CD所成角是60º.(7分)
∵AE⊥BC,PE⊥BC,PE//DC,∴CD⊥BC,∴CE为异面直线AE和CD的公垂线段,(12分)它们之间的距离为1.(14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com