
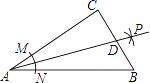
【题目】如图,在Rt△ABC中,∠C=90°,以A为圆心,以任意长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,以大于![]() MN的长为半径画弧,两弧相交于点P,作射线AP交BC于点D,若AC=4,BC=3,则CD的长为( )
MN的长为半径画弧,两弧相交于点P,作射线AP交BC于点D,若AC=4,BC=3,则CD的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
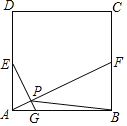
【题目】如图,在正方形ABCD中,E、F分别是AD、BC的中点,![]() ,若
,若![]() ,则下列结论:
,则下列结论:![]() ;
;![]() ;
;![]() ;
;![]() 若M是正方形内任一点,当
若M是正方形内任一点,当![]() 时,
时,![]() 的周长的最小值为
的周长的最小值为![]() ;其中正确的结论
;其中正确的结论![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
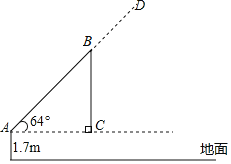
【题目】如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为![]() ,吊臂底部A距地面
,吊臂底部A距地面![]() 参考数据
参考数据![]() ,
,![]() ,
,![]() .
.
![]() 当吊臂底部A与货物的水平距离AC为5m时,吊臂AB的长为______
当吊臂底部A与货物的水平距离AC为5m时,吊臂AB的长为______![]() 计算结果精确到
计算结果精确到![]() ;
;
![]() 如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?
如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?![]() 吊钩的长度与货物的高度忽略不计
吊钩的长度与货物的高度忽略不计![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
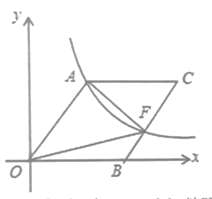
【题目】如图,在直角坐标系中,四边形OACB为菱形,OB在x轴的正半轴上,∠AOB=60°,过点A的反比例函数y= ![]() 的图像与BC交于点F,则△AOF的面积为 ______________.
的图像与BC交于点F,则△AOF的面积为 ______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线W:y=x-4x+2的顶点为A,与x轴交于点B、C.
(1)求∠ABC的正切值;
(2)若点P是抛物线W上的一点,过P作直线PQ垂直x轴,将抛物线W关于直线PQ对称,得到抛物线Wˊ,设抛物线Wˊ的顶点Aˊ,问:是否存在这样的点P,使得△APAˊ为直角三角形?若存在,求出对称所得的抛物线Wˊ的表达式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
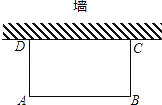
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2 ,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com