
 在如图的直角坐标系中,已知点A(1,0);B(0,-2),将线段AB绕点A按逆时针方向旋转90°至AC.
在如图的直角坐标系中,已知点A(1,0);B(0,-2),将线段AB绕点A按逆时针方向旋转90°至AC.分析 (1)过点C作CD垂直于x轴,由线段AB绕点A按逆时针方向旋转90°至AC,根据旋转的旋转得到AB=AC,且∠BAC为直角,可得∠OAB与∠CAD互余,由∠AOB为直角,可得∠OAB与∠ABO互余,根据同角的余角相等可得一对角相等,再加上一对直角相等,利用ASA可证明三角形ACD与三角形AOB全等,根据全等三角形的对应边相等可得AD=OB,CD=OA,由A和B的坐标及位置特点求出OA及OB的长,可得出OD及CD的长,根据C在第四象限得出C的坐标;
(2)①由已知的抛物线经过点C,把第一问求出C的坐标代入抛物线解析式,列出关于a的方程,求出方程的解得到a的值,确定出抛物线的解析式;
②假设存在点P使△ABP是以AB为直角边的等腰直角三角形,分三种情况考虑:(i)A为直角顶点,过A作AP1垂直于AB,且AP1=AB,过P1作P1M垂直于x轴,如图所示,根据一对对顶角相等,一对直角相等,AB=AP1,利用AAS可证明三角形AP1M与三角形ACD全等,得出AP1与P1M的长,再由P1为第二象限的点,得出此时P1的坐标,代入抛物线解析式中检验满足;(ii)当B为直角顶点,过B作BP2垂直于BA,且BP2=BA,过P2作P2N垂直于y轴,如图所示,同理证明三角形BP2N与三角形AOB全等,得出P2N与BN的长,由P2为第三象限的点,写出P2的坐标,代入抛物线解析式中检验满足;(iii)当B为直角顶点,过B作BP3垂直于BA,且BP3=BA,如图所示,过P3作P3H垂直于y轴,同理可证明三角形P3BH全等于三角形AOB,可得出P3H与BH的长,由P3为第四象限的点,写出P3的坐标,代入抛物线解析式检验,不满足,综上,得到所有满足题意的P的坐标.
解答 解:(1)如图1,过C作CD⊥x轴,垂足为D,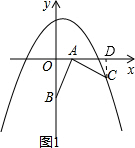
∵BA⊥AC,∴∠OAB+∠CAD=90°,
又∠AOB=90°,∴∠OAB+∠OBA=90°,
∴∠CAD=∠OBA,又AB=AC,∠AOB=∠ADC=90°,
∴△AOB≌△CDA,又A(1,0),B(0,-2),
∴OA=CD=1,OB=AD=2,
∴OD=OA+AD=3,又C为第四象限的点,
∴C的坐标为(3,-1);
(2)①∵抛物线y=-$\frac{1}{2}$x2+ax+2经过点C,且C(3,-1),
∴把C的坐标代入得:-1=-$\frac{9}{2}$+3a+2,解得:a=$\frac{1}{2}$,
则抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+2;
②存在点P,△ABP是以AB为直角边的等腰直角三角形,
(i)若以AB为直角边,点A为直角顶点,
则延长CA至点P1使得P1A=CA,得到等腰直角三角形ABP1,过点P1作P1M⊥x轴,如图2所示,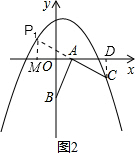
∵AP1=CA,∠MAP1=∠CAD,∠P1MA=∠CDA=90°,
∴△AMP1≌△ADC,
∴AM=AD=2,P1M=CD=1,
∴P1(-1,1),经检验点P1在抛物线y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+2上;
(ii)若以AB为直角边,点B为直角顶点,则过点B作BP2⊥BA,且使得BP2=AB,
得到等腰直角三角形ABP2,过点P2作P2N⊥y轴,如图3,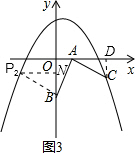
同理可证△BP2N≌△ABO,
∴NP2=OB=2,BN=OA=1,
∴P2(-2,-1),经检验P2(-2,-1)也在抛物线y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+2上;
(iii)若以AB为直角边,点B为直角顶点,则过点B作BP3⊥BA,且使得BP3=AB,
得到等腰直角三角形ABP3,过点P3作P3H⊥y轴,如图4,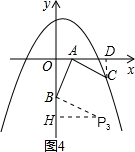
同理可证△BP3H≌△BAO,
∴HP3=OB=2,BH=OA=1,
∴P3(2,-3),经检验P3(2,-3)不在抛物线y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+2上;
则符合条件的点有P1(-1,1),P2(-2,-1)两点.
点评 此题属于二次函数的综合题,涉及的知识有:全等三角形的判定与性质,待定系数法求二次函数的解析式,以及等腰直角三角形的性质等知识.此题综合性强,难度较大,解题的关键是要注意数形结合思想、方程思想与分类讨论思想的应用.


科目:初中数学 来源: 题型:选择题
| A. | 3x-5=x+1移项,得3x-x=1-5 | B. | $\frac{x}{3}$+$\frac{x}{4}$=1去分母,得4x+3x=1 | ||
| C. | 2(x-1)+4=x去括号,得2x-2+4=x | D. | -5x=15的两边同除以-5,得x=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A的坐标(x1,0),点B的坐标(x2,0),已知实数x1,x2(x1<x2)分别是方程x2+2x-3=0的两根,OA=OC,抛物线经过A、B、C三点,记抛物线顶点为点E.
如图,在平面直角坐标系中,点A的坐标(x1,0),点B的坐标(x2,0),已知实数x1,x2(x1<x2)分别是方程x2+2x-3=0的两根,OA=OC,抛物线经过A、B、C三点,记抛物线顶点为点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明不小心敲坏了一块圆形玻璃,于是他拿了其中的一小块到玻璃店去配同样大小的圆形玻璃(如图),店里的师傅说不知圆形玻璃的大小不能配,小明就借了一把尺,先量得其中的一条弦AB的长度为60厘米,然后再量得这个弓形的高CD长度为10厘米,由此就可求得半径解决问题.请你帮小明:
小明不小心敲坏了一块圆形玻璃,于是他拿了其中的一小块到玻璃店去配同样大小的圆形玻璃(如图),店里的师傅说不知圆形玻璃的大小不能配,小明就借了一把尺,先量得其中的一条弦AB的长度为60厘米,然后再量得这个弓形的高CD长度为10厘米,由此就可求得半径解决问题.请你帮小明:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
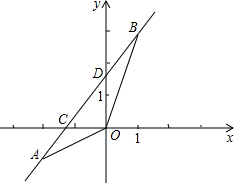 如图,已知一次函数y=kx+b的图象经过A(-2a,-1),B(2-a,3)两点,并且交y轴于点D(0,1.5),且△AOB的面积为$\frac{75}{32}$,则a的值为$\frac{9}{8}$.
如图,已知一次函数y=kx+b的图象经过A(-2a,-1),B(2-a,3)两点,并且交y轴于点D(0,1.5),且△AOB的面积为$\frac{75}{32}$,则a的值为$\frac{9}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com