
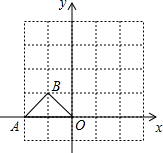
 如图,在平面直角坐标系中,△AOB的顶点A(-2,0)、B(-1,1).将△AOB绕点O顺时针旋转90°后,点A、B分别落在A′、B′.
如图,在平面直角坐标系中,△AOB的顶点A(-2,0)、B(-1,1).将△AOB绕点O顺时针旋转90°后,点A、B分别落在A′、B′. 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
 已知直线l1:y1=2x+3与直线l2:y2=kx-1交于A点,A点横坐标为-1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.
已知直线l1:y1=2x+3与直线l2:y2=kx-1交于A点,A点横坐标为-1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 观察时间 | 10:30(t=0) | 10:36(t=6) | 10:48(t=18) |
| 路牌内容 | 上海90Km | 上海80Km | 上海60Km |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知平行四边形ABCD,AE与BC延长线相交于E、与CD相交于F,
已知平行四边形ABCD,AE与BC延长线相交于E、与CD相交于F,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角为45°的传送带AB,调整为坡度i=1:$\sqrt{3}$的新传送带AC(如图所示).已知原传送带AB的长是4$\sqrt{2}$米.那么新传送带AC的长是8米.
某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角为45°的传送带AB,调整为坡度i=1:$\sqrt{3}$的新传送带AC(如图所示).已知原传送带AB的长是4$\sqrt{2}$米.那么新传送带AC的长是8米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com